题目内容
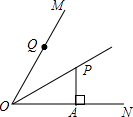如图，如图，OP平分∠MON，PA⊥ON于点A，点Q是射线OM上的一个动点，若PA=10，则PQ的最小值为（ ）| A、5 | B、10 | C、15 | D、20 |
考点：角平分线的性质,垂线段最短
专题：
分析：根据题意点Q是射线OM上的一个动点，要求PQ的最小值，需要找出满足题意的点Q，根据直线外一点与直线上各点连接的所有线段中，垂线段最短，所以我们过点P作PQ垂直OM，此时的PQ最短，然后根据角平分线上的点到角两边的距离相等可得PA=PQ，利用已知的PA的值即可求出PQ的最小值．
解答：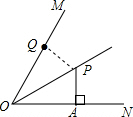
解：过点P作PQ⊥OM，垂足为Q，则PQ为最短距离，
∵OP平分∠MON，PA⊥ON，PQ⊥OM，
∴PA=PQ=10，
故选B．
解：过点P作PQ⊥OM，垂足为Q，则PQ为最短距离，∵OP平分∠MON，PA⊥ON，PQ⊥OM，
∴PA=PQ=10，
故选B．
点评：此题主要考查了角平分线的性质，本题的关键是要根据直线外一点与直线上各点连接的所有线段中，垂线段最短，找出满足题意的点Q的位置．
练习册系列答案
相关题目
下列说法中正确的是（ ）
| A、任何有理数的绝对值都是正数 |
| B、最大的负有理数是-1 |
| C、0是最小的数 |
| D、如果两个数互为相反数，那么它们的绝对值相等 |
下列命题中，其中的真命题是（ ）
| A、27的立方根是±3 |
| B、有两边和一个角分别对应相等的两个三角形全等 |
| C、无限小数是无理数 |
| D、两角和其中的对边对应相等的两个三角形全等 |
下列各对数中不相等的是（ ）
| A、-（-8）与+（+8） |
| B、-（+8）与+|-8| |
| C、-23与（-2）3 |
| D、-|-8|与+（-8） |
已知?ABCD的两邻边上的高AE=2，AF=3，∠B=45°，则?ABCD的面积为若|m-2|+（n-5）2=0，则m-n的值是（ ）
| A、3 | B、-3 | C、7 | D、-7 |