题目内容
20.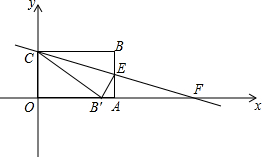 如图,在直角坐标系中放入一个矩形纸片ABCO,将纸片翻折后,点B恰好落在x轴上,记为B',折痕为CE.直线CE的关系式是y=-$\frac{1}{2}$x+8,与x轴相交于点F,且AE=3.
如图,在直角坐标系中放入一个矩形纸片ABCO,将纸片翻折后,点B恰好落在x轴上,记为B',折痕为CE.直线CE的关系式是y=-$\frac{1}{2}$x+8,与x轴相交于点F,且AE=3.(1)求OC长度;
(2)求点B'的坐标;
(3)求矩形ABCO的面积.
分析 (1)在直线y=-$\frac{1}{2}$x+8中令x=0可求得C点坐标,则可求得OC长度;
(2)由折叠的性质可求得B′E,在Rt△AB′E中,可求得AB′,再由点E在直线CF上,可求得E点坐标,则可求得OA长,利用线段和差可求得OB′,则可求得点B′的坐标;
(3)由(1)、(2)可求得OC和OA,可求得矩形ABCO的面积.
解答 解:
(1)∵直线y=-$\frac{1}{2}$x+8与y轴交于点为C,
∴令x=0,则y=8,
∴点C坐标为(0,8),
∴OC=8;
(2)在矩形OABC中,AB=OC=8,∠A=90°,
∵AE=3,
∴BE=AB-BE=8-3=5,
∵是△CBE沿CE翻折得到的,
∴EB′=BE=5,
在Rt△AB′E中,AB′=$\sqrt{B′{E}^{2}-A{E}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4,
由点E在直线y=-$\frac{1}{2}$x+8上,设E(a,3),
则有3=-$\frac{1}{2}$a+8,解得a=10,
∴OA=10,
∴OB′=OA-AB′=10-4=6,
∴点B′的坐标为(0,6);
(3)由(1),(2)知OC=8,OA=10,
∴矩形ABCO的面积为OC×OA=8×10=80.
点评 本题为一次函数的综合应用,涉及直线与坐标轴的交点、轴对称的性质、勾股定理、矩形的性质及方程思想等知识点.在(1)中注意求与坐标轴交点的方法,在(2)中求得E点坐标是解题的关键.本题涉及知识点不多,综合性不强,难度不大,较容易得分.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
5.在2016年“十一”黄金周期间,南京博物馆迎来观众34000人,这个数可用科学记数法表示为( )
| A. | 3.4×103 | B. | 34×103 | C. | 0.34×103 | D. | 3.4×104 |
12.在Rt△ABC中,∠C=90°,sinA=$\frac{3}{5}$,则cosA的值等于( )
| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{\sqrt{5}}{5}$ |
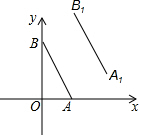 如图,A、B的坐标分别为(2,0),(0,4),若将线段AB平移到A1B1,A1,B1的坐标分别为(4,a),(b,6),则a+b=( )
如图,A、B的坐标分别为(2,0),(0,4),若将线段AB平移到A1B1,A1,B1的坐标分别为(4,a),(b,6),则a+b=( )
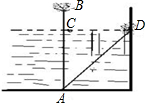 水池中离岸边D点1.5米的C处,直立长着一根芦苇,出水部分BC的长是0.5米,把芦苇拉到岸边,它的顶端B恰好落到D点,并求水池的深度AC.
水池中离岸边D点1.5米的C处,直立长着一根芦苇,出水部分BC的长是0.5米,把芦苇拉到岸边,它的顶端B恰好落到D点,并求水池的深度AC.