题目内容
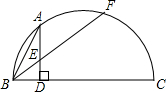如图所示，BC是⊙O直径，AD⊥BC，垂足为D， |
| BA |
|
| AF |
分析：连CF，AC，由在同圆中等弧对的圆周角相等得到∠BCA=∠ACF，∠ACF=∠ABF，由同角的余角相等
得到∠BAD=∠BCA，所以∠ABF=∠BAD，即BE=AE．
得到∠BAD=∠BCA，所以∠ABF=∠BAD，即BE=AE．
解答：
证明：连CF，AC，
∵
=
，
∴∠BCA=∠ACF，∠ACF=∠ABF，
∵BC为圆的直径，∴∠BAC=90°，
∴∠ABC+∠ACB=90°，
又AD⊥BC，∴∠ADB=90°，
∴∠ABC+∠BAD=90°，
∴∠BAD=∠BCA，
∴∠ABF=∠BAD，
即BE=AE．
证明：连CF，AC，∵
|
| BA |
|
| AF |
∴∠BCA=∠ACF，∠ACF=∠ABF，
∵BC为圆的直径，∴∠BAC=90°，
∴∠ABC+∠ACB=90°，
又AD⊥BC，∴∠ADB=90°，
∴∠ABC+∠BAD=90°，
∴∠BAD=∠BCA，
∴∠ABF=∠BAD，
即BE=AE．
点评：本题利用了圆周角定理，在同圆中等弧对的圆周角相等．
练习册系列答案
相关题目
某单位自行车车棚的顶部支架为一个等腰三角形ABC，AB=AC，如图所示．BC是一条水平的横梁，其跨度BC=8米，∠BAC=120°，从顶部A悬挂铅垂线AD，与BC相交于点E．求：
如图所示，BC是⊙O的直径，AD⊥BC，垂足为D，AB=AF，BF和AD相交于点E；
，BF与AD交于E，求证：AE=BE．
，BF与AD交于E，求证：AE=BE．