题目内容
3.如图,在平面直角坐标系xOy中,函数y=ax2+bx+1(a≠0)的图象与x的正半轴交于点A,与x的负半轴交于点B,与y轴交于点C.△PAC中,P(1,-1),∠P=90°,PA=PC.(1)求点A的坐标.
(2)将△PAC沿AC翻折,若点P的对应点Q恰好落在函数y=ax2+bx+1(a≠0)的图象上,求a与b的值.
(3)将△ACO绕点A逆时针旋转90°得到△ADE,在x轴上取一点M,将∠PMD沿PM翻折,若点D的对应点F恰好落在x轴上,求点M的坐标.
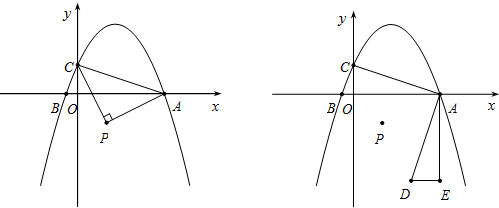
分析 (1)首先求出点C的坐标,根据PA=PC,即可求出点A的坐标;
(2)先求出直线AC的解析式,然后根据点Q和点P关于直线AC对称轴求出点Q的坐标,再列出关于a和b的二元一次方程组,求出a和b的值;
(3)先求出点D的坐标,设点M(m,0),由PD=PF得,F(-1,0)或F(3,0),再根据MD=MF求出m的值.
解答 解:(1)设点A的坐标为(a,0),
∵y=ax2+bx+1,
∴C(0,1),
∵P(1,-1),PA=PC,
∴$\sqrt{1+(-1-1)^{2}}$=$\sqrt{(a-1)^{2}+1}$,
∴a=3或a=-1,
∴点A的坐标为(3,0);
(2)设直线AC的解析式为y=kx+b,
则$\left\{\begin{array}{l}{3k+b=0}\\{b=1}\end{array}\right.$,
解得k=-$\frac{1}{3}$,b=1,
∴直线AC的解析式为y=-$\frac{1}{3}$x+1,
设点Q的坐标为(m,n),
∵点Q和点P关于直线AC对称轴,
∴Q(2,2),
∴$\left\{\begin{array}{l}{9a+3b+1=0}\\{4a+2b+1=2}\end{array}\right.$,
解得a=$-\frac{5}{6}$,b=$\frac{13}{6}$;
(3)解:D(2,-3),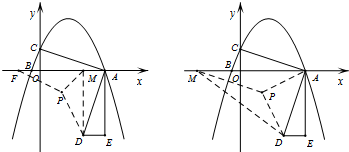
设点M(m,0),
由PD=PF得,F(-1,0)或F(3,0),
当点F(-1,0)时,由MD=MF得,(m-2)2+32=(m+1)2,解得m=2,
当点F(3,0)时,由MD=MF得,(m-2)2+32=(m-3)2,解得m=-2,
因此点M的坐标为(2,0)或(-2,0).
点评 本题主要考查了二次函数的综合题,此题涉及到了翻折变换、待定系数法求一次函数解析式、勾股定理等知识,解答本题的关键是熟练掌握对称的性质,此题有一定的难度.

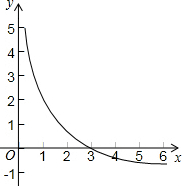 小颖画了一个函数y=$\frac{a}{x}$-1的图象如图,那么关于x的分式方程$\frac{a}{x}$=1的解是( )
小颖画了一个函数y=$\frac{a}{x}$-1的图象如图,那么关于x的分式方程$\frac{a}{x}$=1的解是( )| A. | x=1 | B. | x=2 | C. | x=3 | D. | x=4 |
| A. | 6 | B. | $\sqrt{6}$ | C. | 2 | D. | $\sqrt{2}$ |
| A. | (a3-a)÷a=a2 | B. | (a3)2=a5 | C. | a3+a2=a5 | D. | a3÷a3=1 |
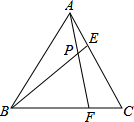 如图,等边三角形ABC的边长为6,点E、点F分别是AC、BC边上的点,连接AF,BE交于点P.给出以下判断:
如图,等边三角形ABC的边长为6,点E、点F分别是AC、BC边上的点,连接AF,BE交于点P.给出以下判断: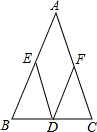 如图,已知:在△ABC中,AB=AC,D为BC的中点,E、F分别是AB、AC边上的点,且BE=CF.求证:DE=DF.
如图,已知:在△ABC中,AB=AC,D为BC的中点,E、F分别是AB、AC边上的点,且BE=CF.求证:DE=DF.