Question

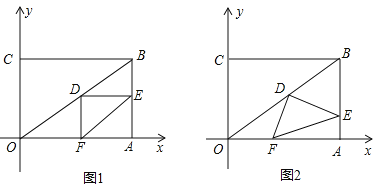
【题目】如图，抛物线y=ax2+bx﹣5（a≠0）与x轴交于点A（﹣5，0）和点B（3，0），与y轴交于点C．

（1）求该抛物线的解析式；

（2）若点E为x轴下方抛物线上的一动点，当S△ABE=S△ABC时，求点E的坐标；

（3）在（2）的条件下，抛物线上是否存在点P，使∠BAP=∠CAE？若存在，求出点P的横坐标；若不存在，请说明理由．

Answer 1

【答案】(1)y=x2+x﹣5；(2)E点坐标为（﹣2，﹣5）；(3)存在满足条件的点P，其横坐标为或

．

【解析】

（1）把A、B两点的坐标代入，利用待定系数法可求得抛物线的解析式；（2）当S△ABE=S△ABC时，可知E点和C点的纵坐标相同，可求得E点坐标；（3）在△CAE中，过E作ED⊥AC于点D，可求得ED和AD的长度，设出点P坐标，过P作PQ⊥x轴于点Q，由条件可知△EDA∽△PQA，利用相似三角形的对应边可得到关于P点坐标的方程，可求得P点坐标．

（1）把A、B两点坐标代入解析式可得，，解得 ，

∴抛物线解析式为y=x2+x﹣5；

（2）在y=x2+x﹣5中，令x=0可得y=﹣5，

∴C（0，﹣5），

∵S△ABE=S△ABC，且E点在x轴下方，

∴E点纵坐标和C点纵坐标相同，

当y=﹣5时，代入可得x2+x=﹣5，解得x=﹣2或x=0（舍去），

∴E点坐标为（﹣2，﹣5）；

（3）假设存在满足条件的P点，其坐标为（m，m2+m﹣5），

如图，连接AP、CE、AE，过E作ED⊥AC于点D，过P作PQ⊥x轴于点Q，

则AQ=AO+OQ=5+m，PQ=|m2+m﹣5|，

在Rt△AOC中，OA=OC=5，则AC=，∠ACO=∠DCE=45°，

由（2）可得EC=2，在Rt△EDC中，可得DE=DC=，

∴AD=AC﹣DC=﹣=4，

当∠BAP=∠CAE时，则△EDA∽△PQA，

∴，即=，

∴m2+m﹣5=（5+m）或m2+m﹣5=﹣（5+m），

当m2+m﹣5=（5+m）时，整理可得4m2﹣5m﹣75=0，解得m=或m=﹣5（与A点重合，舍去），

当m2+m﹣5=﹣（5+m）时，整理可得4m2+11m﹣45=0，解得m=或m=﹣5（与A点重合，舍去），

∴存在满足条件的点P，其横坐标为或．