题目内容
小明、小芳做一个“配色”的游戏.右图是两个可以自由转动的转盘,每个转盘被分成面积相等的几个扇形,并涂 上图中所示的颜色.同时转动两个转盘,如果转盘
上图中所示的颜色.同时转动两个转盘,如果转盘 转出了红色,转盘
转出了红色,转盘 转出了蓝色,或者转盘
转出了蓝色,或者转盘 转出了蓝色,转盘
转出了蓝色,转盘 转出了红色,则红色和蓝色在一起配成紫
转出了红色,则红色和蓝色在一起配成紫 色,这种情
色,这种情 况下小芳获胜;同样,蓝色和黄色在一起配成绿色,这种情
况下小芳获胜;同样,蓝色和黄色在一起配成绿色,这种情 况下小明获胜;在其它情况下,则小明、小芳不分胜负.
况下小明获胜;在其它情况下,则小明、小芳不分胜负.
(1)利用列表或树状图的方法表示此游戏所有可能出现的结果;
(2)此游戏的规则,对 小明、小芳公平吗?试说明理由.
小明、小芳公平吗?试说明理由.
 |
解:用列表法将 所有可能出现的结果表示如下:
所有可能出现的结果表示如下:
|
转盘A | 红 | 蓝 | 黄 |
| 红 | (红,红) | (红,蓝) | (红,黄) |
| 蓝 | (蓝,红) | (蓝,蓝) | (蓝,黄) |
| 红 | (红,红) | (红,蓝) | (红,黄) |
| 黄 | (黄,红) | (黄,蓝) | (黄, |
所以,所有可能出现的结果共有12种.
(2)上面等可能出现的12种结果中,有3种情况可能得到紫色, 故配成紫色的概率是
故配成紫色的概率是 ,即小芳获胜的概率是
,即小芳获胜的概率是 ;但只有2种情况才可能得到绿色,配成绿色的概率是
;但只有2种情况才可能得到绿色,配成绿色的概率是 ,即小明获胜的概率是
,即小明获胜的概率是 .而
.而 ,故小芳获胜的可能性大,这个“配色”游戏对小明、小芳双方是不公平的.
,故小芳获胜的可能性大,这个“配色”游戏对小明、小芳双方是不公平的.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 转盘B
转盘B  -
- ;
;
 队和韩国队等9支球队参加奥运会足球预
队和韩国队等9支球队参加奥运会足球预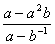 结果是 ( )
结果是 ( ) (B)
(B) (C)
(C)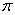 (D)2
(D)2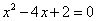 ,下列配方正确的是( )
,下列配方正确的是( )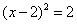 B.
B.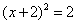 C.
C.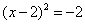 D.
D.