��Ŀ����
ij�����м���ԭ��69ǧ�ˣ�����ԭ��52ǧ�ˣ��ּƻ���������ԭ������A��B�����ͺŵIJ�Ʒ��80������֪ÿ��A�ͺŲ�Ʒ��Ҫ����ԭ��0.6ǧ�ˣ�����ԭ��0.9ǧ�ˣ�ÿ��B�ͺŲ�Ʒ��Ҫ����ԭ��1.1ǧ�ˣ�����ԭ��0.4ǧ�ˣ������������⣺
��1���ù������ļ�������������
��2����������Ʒȫ���۳��������£���1��A�ͺŲ�Ʒ����35Ԫ��1��B�ͺŲ�Ʒ����25Ԫ����1�������ַ������������������Ƕ��٣�
��3���ڣ�2���������£��������������������25%ȫ�������ٴι����ס�������ԭ�ϣ�Ҫ��ÿ��ԭ�����ٹ���4ǧ�ˣ��ҹ���ÿ��ԭ�ϵ�������Ϊ������������ԭ��ÿǧ��40Ԫ������ԭ��ÿǧ��60Ԫ����ֱ��д������ס�������ԭ��֮�����ķ�����
�⣺��1��������A�ͺŲ�Ʒx����������B�ͺŲ�Ʒ��80��x�����������⣬��
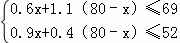 ��
��
��ã�38��x��40��
��x������
��x=38��39��40��
����3�ֹ�����
����1������A�ͺŲ�Ʒ38��������B�ͺŲ�Ʒ42����
����2������A�ͺŲ�Ʒ39��������B�ͺŲ�Ʒ41����
����3������A�ͺŲ�Ʒ40��������B�ͺŲ�Ʒ40����
��2������������ΪWԪ�������⣬��
W=35x+25��80��x����
w=10x+2000��
��k=10��0��
��W��x�����������
�൱x=40ʱ��W���=2400Ԫ��
������A�ͺŲ�Ʒ40����B�ͺŲ�Ʒ40��ʱ��������������Ϊ2400Ԫ��
��3���蹺�����ԭ��mǧ�ˣ���������ԭ��nǧ�ˣ������⣬��
40m+60n=2400
2m+3n=120��
��m+nҪ���
��nҪ��С��
��m��4��n��4��
��n=4��
��m=9��
�߹������ԭ��9ǧ�ˣ�����ԭ��4ǧ�ˣ�

��֪ �Ƿ�����
�Ƿ����� �Ľ⣬��a��b��ֵ�ǣ�������
�Ľ⣬��a��b��ֵ�ǣ�������
| �� | A�� | ��1 | B�� | 2 | C�� | 3 | D�� | 4 |
 ����ô�����ж���ȷ���ǣ� ��
����ô�����ж���ȷ���ǣ� �� B��
B�� C��
C�� D��
D�� ��
��
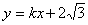 ��y���ڵ�A���뷴��������
��y���ڵ�A���뷴��������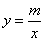 ��ͼ���ڵ�C��3��n����
��ͼ���ڵ�C��3��n����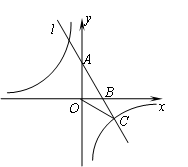
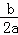 ��
��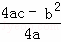 ����
����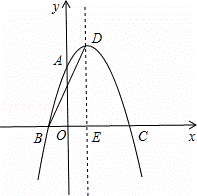
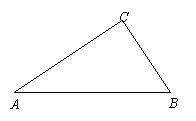 ��3����֤��BC=E.D
��3����֤��BC=E.D