题目内容
 如图,矩形ABCD内接于⊙O,且AB=
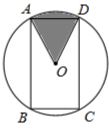
如图,矩形ABCD内接于⊙O,且AB= ,BC=1,则图中阴影部分所表示的扇形AOD的面积为
,BC=1,则图中阴影部分所表示的扇形AOD的面积为
- A.

- B.

- C.

- D.

C
分析:连接AC可求AC=2,∠B=90°,AC为直径,△AOD为等边三角形,∠AOD=60°,可求扇形面积.
解答: 解:连接AC.
解:连接AC.
∵Rt△ABC中,∠ABC=90°,AB= ,BC=1,
,BC=1,
∴AC=2,OA=1,
∴△AOD为等边三角形,∠AOD=60°,
∴SAOD= =
= ,
,
故选C.
点评:此题考查勾股定理,等边三角形判定,扇形面积求法.
分析:连接AC可求AC=2,∠B=90°,AC为直径,△AOD为等边三角形,∠AOD=60°,可求扇形面积.
解答:
 解:连接AC.
解:连接AC.∵Rt△ABC中,∠ABC=90°,AB=
 ,BC=1,
,BC=1,∴AC=2,OA=1,
∴△AOD为等边三角形,∠AOD=60°,
∴SAOD=
 =
= ,
,故选C.
点评:此题考查勾股定理,等边三角形判定,扇形面积求法.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
 如图,矩形ABCD内接于⊙O,且AB=
如图,矩形ABCD内接于⊙O,且AB=| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|

 如图,矩形ABCD内接于⊙O,且AB=
如图,矩形ABCD内接于⊙O,且AB= (2012•沙河口区模拟)如图,矩形ABCD内接于⊙O,且AB=
(2012•沙河口区模拟)如图,矩形ABCD内接于⊙O,且AB= (2012•桂平市三模)如图,矩形ABCD内接于⊙O,AB=3AD,对角线AC中点O为圆心,BK⊥AC,垂足为K.DH∥KB,DH分别与AC、AB、⊙O及CB的延长线相交于点E、F、G、H.
(2012•桂平市三模)如图,矩形ABCD内接于⊙O,AB=3AD,对角线AC中点O为圆心,BK⊥AC,垂足为K.DH∥KB,DH分别与AC、AB、⊙O及CB的延长线相交于点E、F、G、H.