题目内容
已知在等腰△ABC中,AB=AC,在射线CA上截取线段CE,在射线AB上截取线段BD,连接DE,DE所在直线交直线BC与点M。请探究:
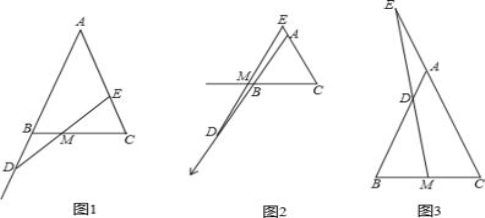
(1)如图(1),当点E在线段AC上,点D在AB延长线上时,若BD=CE,请判断线段MD和线段ME的数量关系,并证明你的结论。
(2)如图(2),当点E在CA的延长线上,点D在AB的延长线上时,若BD=CE,则(1)中的结论还成立吗?如果成立,请证明;如果不成立,说明理由;
(3)如图(3),当点E在CA的延长线上,点D在线段AB上(点D不与A,B重合),DE所在直线与直线BC交于点M,若CE=2BD,请直接写出线段MD与线段ME的数量关系。
(1)DM=EM.理由见解析;(2)成立,理由见解析;(3)MD=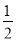 ME.
ME.
【解析】
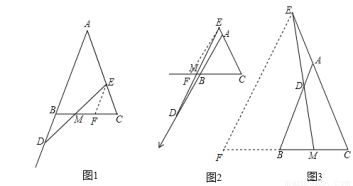
试题分析:(1)DM=EM;过点E作EF∥AB交BC于点F,然后利用平行线的性质和已知条件可以证明△DBM≌△EFM,接着利用全等三角形的性质即可证明题目的结论;
(2)成立;过点E作EF∥AB交CB的延长线于点F,然后利用平行线的性质与已知条件可以证明△DBM≌△EFM,接着利用全等三角形的性质即可证明题目的结论;
(3)MD=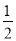 ME.过点E作EF∥AB交CB的延长线于点F,然后利用平行线的性质和已知条件得到△DBM∽△EFM,接着利用相似三角形的性质即可得到结论;
ME.过点E作EF∥AB交CB的延长线于点F,然后利用平行线的性质和已知条件得到△DBM∽△EFM,接着利用相似三角形的性质即可得到结论;
试题解析:(1)DM=EM;(1分)
证明:过点E作EF∥AB交BC于点F,(2分)
∵AB=AC,
∴∠ABC=∠C;
又∵EF∥AB,
∴∠ABC=∠EFC,
∴∠EFC=∠C,
∴EF=EC.
又∵BD=EC,
∴EF=BD.
又∵EF∥AB,
∴∠ADM=∠MEF.
在△DBM和△EFM中
 ,
,
∴△DBM≌△EFM,
∴DM=EM.
(2)成立;
证明:过点E作EF∥AB交CB的延长线于点F,
∵AB=AC,
∴∠ABC=∠C;
又∵EF∥AB,
∴∠ABC=∠EFC,
∴∠EFC=∠C,
∴EF=EC.
又∵BD=EC,
∴EF=BD.
又∵EF∥AB,
∴∠ADM=∠MEF.
在△DBM和△EFM中

∴△DBM≌△EFM;
∴DM=EM;
(3)过点E作EF∥AB交CB的延长线于点F,
∴△DBM∽△EFM,
∴BD:EF=DM:ME,
∵AB=AC,
∴∠ABC=∠C,
∵∠F=∠ABC,
∴∠F=∠C,
∴EF=EC,
∴BD:EC=DM:ME=1:2,
∴MD=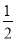 ME.
ME.
考点:全等三角形的判定与性质.


 的图象,在每个象限内,y的值随x值的增大而增大,则k可以为( )
的图象,在每个象限内,y的值随x值的增大而增大,则k可以为( )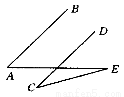


 表示运算ac-bd.
表示运算ac-bd.
 的值;
的值;
 =2,求bd的值.
=2,求bd的值.