题目内容
在矩形ABCD中,点P在AD上,AB=2,AP=1,将三角板的直角顶点放在点P处,三角板的两直角边分别能与AB、BC边相交于点E、F,连接EF.
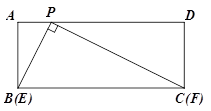
(1)如图,当点E与点B重合时,点F恰好与点C重合,求此时PC的长;
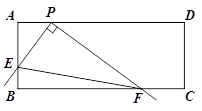
(2)将三角板从(1)中的位置开始,绕点P顺时针旋转,当点E与点A重合时停止,在这个过程中,请你观察、探究并解答:
①∠PEF的大小是否发生变化?请说明理由;
②直接写出从开始到停止,线段EF的中点所经过的路线长.
(1)如图,当点E与点B重合时,点F恰好与点C重合,求此时PC的长;

(2)将三角板从(1)中的位置开始,绕点P顺时针旋转,当点E与点A重合时停止,在这个过程中,请你观察、探究并解答:

①∠PEF的大小是否发生变化?请说明理由;
②直接写出从开始到停止,线段EF的中点所经过的路线长.
(1)PC=2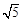 ;(2)①∠PEF的大小不变.②
;(2)①∠PEF的大小不变.②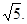
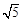 ;(2)①∠PEF的大小不变.②
;(2)①∠PEF的大小不变.②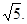
试题分析:(1)先根据勾股定理求得PB的长,再利用互余关系证得△APB∽△DCP,最后根据相似三角形的性质及即可求得结果;
(2)①过F作FG⊥AD,垂足为G,同(1)的方法证明△APB∽△DCP,得相似比
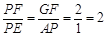 ,再利用锐角三角函数的定义求值;
,再利用锐角三角函数的定义求值;②如图3,画出起始位置和终点位置时,线段EF的中点O1,O2,连接O1O2,线段O1O2即为线段EF的中点经过的路线长,也就是△BPC的中位线.
(1)在矩形ABCD中,
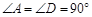 ,AP=1,CD=AB=2,
,AP=1,CD=AB=2,∴PB=
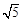 ,
,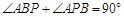 .
.∵
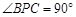 ,
,∴
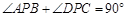 .
.∴
 .
.∴ △ABP∽△DPC.
∴
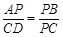 ,即
,即 .
.∴PC=2
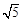 ;
;(2)①∠PEF的大小不变.
理由:过点F作FG⊥AD于点G.
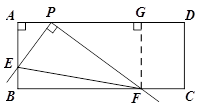
∴四边形ABFG是矩形
∴
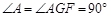
∴GF=AB=2,
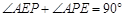
∵
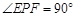
∴
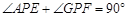
∴
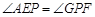
∴ △APE∽△GFP
∴
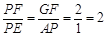
∴在Rt△EPF中,tan∠PEF=

即tan∠PEF的值不变
∴∠PEF的大小不变.
②如图所示:

设线段EF的中点为O,连接OP,OB,
∵在Rt△EPF中,OP=
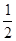 EF,
EF,在Rt△EBF中,OB=
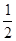 EF,
EF,∴OP=OB=
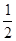 EF,
EF,∴O点在线段BP的垂直平分线上,
∴线段EF的中点经过的路线长为
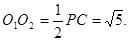
点评:解答本题的关键是熟记相似三角形的对应边成比例,注意对应字母写在对应位置上.

练习册系列答案
相关题目
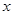 .
. ,并说明理由。
,并说明理由。
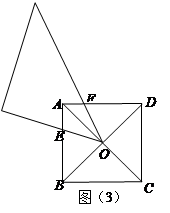
 ,求
,求


 成立吗?请说明理由.
成立吗?请说明理由. 的边AB、AC上的点,DE//BC,
的边AB、AC上的点,DE//BC, ,则
,则 的值是___.
的值是___.
 ,则
,则 ___________。
___________。