题目内容
 如图,将长为2.5米长的梯子AB斜靠在墙上,BC长为0.7米.
如图,将长为2.5米长的梯子AB斜靠在墙上,BC长为0.7米.(1)求梯子上端A到墙的底端C的距离(即AC的长);
(2)如果梯子的顶端A沿墙下滑0.4米(即AA′=0.4米),则梯脚B将外移(即BB′的长)多少米?
分析:(1)在Rt△ABC中利用勾股定理求出AC的长即可;
(2)由(1)可以得出梯子的初始高度,下滑0.4米后,可得出梯子的顶端距离地面的高度,再次使用勾股定理,已知梯子的底端距离墙的距离为0.7米,可以得出,梯子底端水平方向上滑行的距离.
(2)由(1)可以得出梯子的初始高度,下滑0.4米后,可得出梯子的顶端距离地面的高度,再次使用勾股定理,已知梯子的底端距离墙的距离为0.7米,可以得出,梯子底端水平方向上滑行的距离.
解答:解:(1)在Rt△ABC中,∠C=90°,AC=
=2.4(米);
(2)∵A′C=AC-AA′=2.4-0.4=2(米),A′B′=2.5(米),
∴B′C=
=1.5(米),
∴B′B=B′C-BC=1.5-0.7=0.8(米)
答:梯脚B将外移(即BB′的长)0.8米.
| AB2-BC2 |
(2)∵A′C=AC-AA′=2.4-0.4=2(米),A′B′=2.5(米),
∴B′C=
| A′B′2-A′C2 |
∴B′B=B′C-BC=1.5-0.7=0.8(米)
答:梯脚B将外移(即BB′的长)0.8米.
点评:本题考查正确运用勾股定理.善于观察题目的信息是解题以及学好数学的关键.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
 如图,边长为12米的正方形池塘的周围是草地,池塘边A、B、C、D处各有一棵树,且AB=BC=CD=3米.现用长4米的绳子将一头羊拴在其中的一棵树上.为了使羊在草地上活动区域的面积最大,应将绳子拴在( )
如图,边长为12米的正方形池塘的周围是草地,池塘边A、B、C、D处各有一棵树,且AB=BC=CD=3米.现用长4米的绳子将一头羊拴在其中的一棵树上.为了使羊在草地上活动区域的面积最大,应将绳子拴在( )
 ≈1.8,
≈1.8, 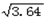 ≈1.9,
≈1.9,  ≈2.1).
≈2.1). 如图,将长为2.5米长的梯子AB斜靠在墙上,BC长为0.7米.
如图,将长为2.5米长的梯子AB斜靠在墙上,BC长为0.7米. (2)(5分)如果梯子的顶端A沿墙下滑0.4米(即AA′=0.4米),则梯脚B将外移
(2)(5分)如果梯子的顶端A沿墙下滑0.4米(即AA′=0.4米),则梯脚B将外移