题目内容
6.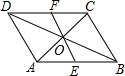 如图,AB∥CD,且AB=CD,AC交DB于点O,过点O的直线EF分别交AB、CD与点E、F,则图中全等的三角形有( )
如图,AB∥CD,且AB=CD,AC交DB于点O,过点O的直线EF分别交AB、CD与点E、F,则图中全等的三角形有( )| A. | 6对 | B. | 5对 | C. | 4对 | D. | 3对 |
分析 根据平行四边形的性质所能得到的相等边和相等角来判断图中有多少全等的三角形.
解答 解:∵AB∥CD,且AB=CD,
∴四边形ABCD是平行四边形,
∴AD=BC,AB=CD,OA=OC,OD=OB;
∠OAB=∠OCD,∠OBD=∠ODC;
①∵AD=BC,AB=CD,BD=BD,
∴△ABD≌△CDB(SSS);同理可证得:△ABC≌△CDA.
②∵OA=OC,OB=OD,AB=CD,
∴△OAB≌△OCD(SSS);同理可证得:△OAD≌△OCB.
③∵OA=OC,∠OAB=∠OCD,∠AOE=∠COF,
∴△AOE≌△COF(ASA);同理可证得:△BOE≌△DOF.
所以图中共有6对全等三角形.
故选A.
点评 本题考查的是平行四边形的性质以及全等三角形的判定,平行四边形基本性质:①平行四边形两组对边分别平行;②平行四边形的两组对边分别相等;③平行四边形的两组对角分别相等;④平行四边形的对角线互相平分.

练习册系列答案
相关题目
17.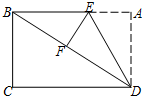 如图,将矩形纸片ABCD折叠,使边AD落在对角线BD上,折痕为DE,且A点落在对角线F处.若AD=3,CD=4,则AE的长为( )
如图,将矩形纸片ABCD折叠,使边AD落在对角线BD上,折痕为DE,且A点落在对角线F处.若AD=3,CD=4,则AE的长为( )
 如图,将矩形纸片ABCD折叠,使边AD落在对角线BD上,折痕为DE,且A点落在对角线F处.若AD=3,CD=4,则AE的长为( )
如图,将矩形纸片ABCD折叠,使边AD落在对角线BD上,折痕为DE,且A点落在对角线F处.若AD=3,CD=4,则AE的长为( )| A. | $\frac{3}{2}$ | B. | 1 | C. | 2 | D. | $\frac{3}{4}$ |
14.在△ADB和△ADC中,下列条件不能得出△ADB≌△ADC的是( )
| A. | BD=DC,AB=AC | B. | ∠B=∠C,∠BAD=∠CAD | C. | ∠B=∠C,BD=DC | D. | AB=AC,∠BAD=∠CAD |
11. 在数轴上表示a、b两数的点如图所示,则下列判断正确的是( )
在数轴上表示a、b两数的点如图所示,则下列判断正确的是( )
 在数轴上表示a、b两数的点如图所示,则下列判断正确的是( )
在数轴上表示a、b两数的点如图所示,则下列判断正确的是( )| A. | a+b>0 | B. | a+b<0 | C. | a>|b| | D. | |a|>|b| |
18.下列说法中正确的是( )
| A. | 有最小的自然数,也有最小的整数 | |
| B. | 没有最小的正数,但有最小的正整数 | |
| C. | 没有最小的负数,但有最小的正数 | |
| D. | 0是最小的整数 |
15.若等腰三角形的两边分别是一元二次方程x2-7x+12=0的两根,则等腰三角形的周长为( )
| A. | 10 | B. | 11 | C. | 10或11 | D. | 以上都不对 |
 如图是某几何体的三视图,该几何体是三棱柱.
如图是某几何体的三视图,该几何体是三棱柱. 如图,在正方形ABCD中,AB=2,E是AD边上一点(点E与点A,D不重合),BE的垂直平分线交AB于M,交DC于N,设AE=x.
如图,在正方形ABCD中,AB=2,E是AD边上一点(点E与点A,D不重合),BE的垂直平分线交AB于M,交DC于N,设AE=x.