题目内容
 如图,等腰梯形ABCD的底边AD在x轴上,顶点C在y轴正半轴上,B(4,2),一次函数y=kx-1的图象平分它的面积,则k的值为( )
如图,等腰梯形ABCD的底边AD在x轴上,顶点C在y轴正半轴上,B(4,2),一次函数y=kx-1的图象平分它的面积,则k的值为( )| A、1 | ||
B、
| ||
| C、-1 | ||
| D、2 |
考点:等腰梯形的性质,待定系数法求一次函数解析式
专题:
分析:过B作BE⊥AD于E,连接OB、CE交于点P,根据等腰梯形的性质可得OD=AE,从而可得出AD的长,这样即可求出中位线的长,然后判断出一次函数经过点P(2,1),利用待定系数法求解k的值即可.
解答:解:过B作BE⊥AD于E,连接OB、CE交于点P,
∵四边形ABCD是等腰梯形,
∴OD=AE,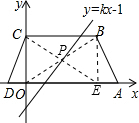
∴AD=OD+OE+AE=2OD+BC=6,
故中位线的长度=
(BC+AD)=5;
又∵Rt△ODC≌Rt△EAB(HL),
∴△ODC和△EAB的面积相等,
由图可知P为矩形OCBE的对称中心,则过P点的直线平分矩形OCBE的面积,
故可得一次函数y=kx-1的图象经过点P,
∵点B(4,2),O(0,0),
∴P点坐标为(2,1),
代入得:2k-1=1,
解得:k=1.
故选A.
∵四边形ABCD是等腰梯形,
∴OD=AE,

∴AD=OD+OE+AE=2OD+BC=6,
故中位线的长度=
| 1 |
| 2 |
又∵Rt△ODC≌Rt△EAB(HL),
∴△ODC和△EAB的面积相等,
由图可知P为矩形OCBE的对称中心,则过P点的直线平分矩形OCBE的面积,
故可得一次函数y=kx-1的图象经过点P,
∵点B(4,2),O(0,0),
∴P点坐标为(2,1),
代入得:2k-1=1,
解得:k=1.
故选A.
点评:此题考查了一次函数及等腰梯形的知识,解答本题的关键在于判断出一次函数图象经过点P.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
若a>0,b<0,c<0,则方程ax2+bx+c=0的根的情况为( )
| A、有两个同号的实数根 |
| B、有两个异号的实数根,且负根的绝对值大 |
| C、有两个异号的实数根,且正根的绝对值大 |
| D、无实数根 |
 如图,在△ABC中,按要求完成下列各题.
如图,在△ABC中,按要求完成下列各题. 如图,以Rt△ABC的三边为边向外作正方形,其面积分别为S1,S2,S3,且S1=4,S2=8,求AB的长.
如图,以Rt△ABC的三边为边向外作正方形,其面积分别为S1,S2,S3,且S1=4,S2=8,求AB的长.