题目内容
10.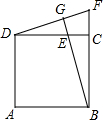 如图所示,在正方形ABCD中,E为CD上一点,延长BC至F,使CF=CE,连接DF,BE与DF相交于点G,则下面结论错误的是( )
如图所示,在正方形ABCD中,E为CD上一点,延长BC至F,使CF=CE,连接DF,BE与DF相交于点G,则下面结论错误的是( )| A. | BE=DF | B. | BG⊥DF | C. | ∠F+∠CEB=90° | D. | ∠FDC+∠ABG=90° |
分析 根据题意可知△BCE≌△DCF,根据全等三角形的性质即可得到答案.
解答 解:∵四边形ABCD是正方形
∴∠BCD=∠ABC=90°,BC=CD,
在△BCE和△DCF中,
$\left\{\begin{array}{l}{BC=CD}\\{∠BCD=∠DCF=90°}\\{CE=CF}\end{array}\right.$,
∴△BCE≌△DCF
∴BE=DF,∠F=∠CEB,∠CBE=∠FDC,
∴∠FBG+∠F=90°(BG⊥DF),∠FDC+∠ABG=90°.
故选:C.
点评 此题考查了正方形的性质和全等三角形的判定与性质,充分利用正方形的特殊性质来找到全等的条件从而判定全等,进一步利用全等三角形的性质解题.

练习册系列答案
相关题目
1.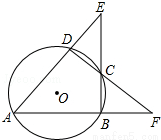 如图,⊙O的内接四边形ABCD的两组对边的延长线分别交于点E、F,若∠E=α,∠F=β,则∠A等于( )
如图,⊙O的内接四边形ABCD的两组对边的延长线分别交于点E、F,若∠E=α,∠F=β,则∠A等于( )
 如图,⊙O的内接四边形ABCD的两组对边的延长线分别交于点E、F,若∠E=α,∠F=β,则∠A等于( )
如图,⊙O的内接四边形ABCD的两组对边的延长线分别交于点E、F,若∠E=α,∠F=β,则∠A等于( )| A. | α+β | B. | $\frac{α+β}{2}$ | C. | 180°-α-β | D. | $\frac{180°-α-β}{2}$ |
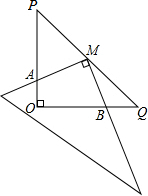 如图,在Rt△POQ中,OP=OQ=4,M是PQ的中点,把一三角尺的直角顶点放在M处,以M为旋转中心,旋转三角尺,三角尺的两直角边与△POQ的两直角边分别交于点A、B.
如图,在Rt△POQ中,OP=OQ=4,M是PQ的中点,把一三角尺的直角顶点放在M处,以M为旋转中心,旋转三角尺,三角尺的两直角边与△POQ的两直角边分别交于点A、B.