题目内容
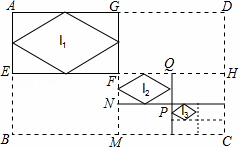
如图10,在平面直角坐标系中,点A(2,n),B(m,n)(m>2),D(p,q)(q<n),点B,D在直线y=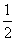 x+1上.四边形ABCD的对角线AC,BD相交于点E,且AB∥CD,
x+1上.四边形ABCD的对角线AC,BD相交于点E,且AB∥CD,
CD=4,BE=DE,△AEB的面积是2.
求证:四边形ABCD是矩形.
 |
解1:∵ AB∥CD,
∴∠EAB=∠ECD,∠EBA=∠EDC.
∵ BE=DE,
∴ △AEB≌△CED.
∴ AB=CD=4.
∵AB∥CD,
∴四边形ABCD是平行四边形.
A(2,n),B(m,n)(m>2),
∴ AB∥x轴,且CD∥x轴.
∵ m>2,∴m=6. 
∴n=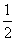 ×6+1=4.
×6+1=4.
∴ B(6,4).
∵△AEB的面积是2,
∴△AEB的高是1.
∴平行四边形ABCD的高是2.
∵ q<n,
∴q=2.
∴p=2,
即D(2,2).
∵点A(2,n),
∴DA∥y轴.
∴AD⊥CD,即∠ADC=90°.
∴四边形ABCD是矩形. 
解2:∵AB∥CD,
∴∠EAB= ∠ECD,∠EBA=∠EDC.
∠ECD,∠EBA=∠EDC.
∵ BE=DE,
∴ △AEB≌△CED.
∴ AB=CD=4.
∵AB∥CD,
∴四边形ABCD是平行四边形.
∵A(2,n),B(m,n)(m>2),
∴ AB∥x轴,且CD∥x轴.
∵ m>2,∴m=6.
∴n=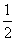 ×6+1=4.
×6+1=4.
∴ B(6,4).
过点E作EF⊥AB,垂足为F,
∵△AEB的面积是2,
∴EF=1. ∵ q<n,
∴点E的纵坐标是3.
∴点E的横坐标是4.
∴ 点F的横坐标是4.
点F的横坐标是4.
∴点F是线段AB的中点.
∴直线EF是线段AB的中垂线.
∴EA=EB.
∵四边形ABCD是平行四边形,
∴AE=EC,BE=ED.
∴AC=BD.
∴四边形ABCD是矩形.

 名校课堂系列答案
名校课堂系列答案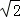 ≈1.41,
≈1.41,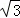 ≈1.73)
≈1.73)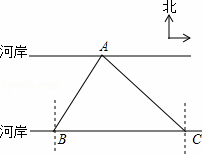
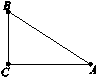
 ,E分别在边AB,AC上,若DE∥BC,
,E分别在边AB,AC上,若DE∥BC, AD=3 ,AB=5,求
AD=3 ,AB=5,求 的值.
的值.

 B.
B.  C.
C.  D.
D. 

 B.
B.  C.
C.  D.
D.