题目内容
2．
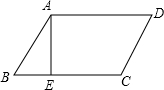如图所示，在?ABCD中，E是BC边上的三分之一点，则S△ABC：S?ABCD的值为（ ）| A． | ${\;}_{\frac{1}{2}}$ | B． | $\frac{1}{4}$ | C． | $\frac{1}{6}$ | D． | $\frac{1}{8}$ |
分析 过点A作AF⊥BC于点F，根据三角形的面积公式和平行四边形的面积公式分别表示出则S△ABC和S?ABCD的面积，再计算即可．
解答 解：过点A作AF⊥BC于点F，
∵E是BC边上的三分之一点，
∴BE：BC=1：3，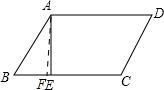
∵S△ABC=$\frac{1}{2}$BE•AF，S?ABCD=BC•AF，
∴S△ABC：S?ABCD=1：6，
故选C．
点评 本题考查了平行四边形的性质以及三角形面积公式和平行四边形的面积公式运用，解题的关键是理解作出三角形的高线同时也是平行四边形的高线．
练习册系列答案
名校通行证有效作业系列答案
相关题目
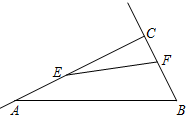如图，在Rt△ABC中，∠ACB=90°，AC=10cm，BC=5cm，点E从点C出发沿射线CA以每秒2cm的速度运动，同时点F从点B出发沿射线BC以每秒1cm的速度运动．设运动时间为t秒．
10．下列条件之一能使菱形ABCD是正方形的为（ ）
①AC⊥BD ②∠BAD=90° ③AB=BC ④AC=BD．
①AC⊥BD ②∠BAD=90° ③AB=BC ④AC=BD．
| A． | ①③ | B． | ②③ | C． | ②④ | D． | ①②③ |
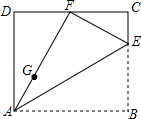如图，将矩形纸片ABCD沿直线AE折叠，点B恰好落在线段CD的中点F上，点G是线段AF上一动点（不与A，F重合），点G过GH⊥AB，垂足为H，将矩形沿直线GH翻折，点A恰好落在线段BH上点A′处．若AB长为8，则当△A′GE为直角三角形时，AH的长为$\frac{24-8\sqrt{3}}{3}$．
14．二次根式$\sqrt{a+1}$中，字母a的取值范围为（ ）
| A． | a≥-1 | B． | a≥0 | C． | a≥1 | D． | a≤-1 |
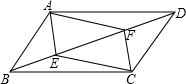如图，E，F是?ABCD对角线上的两点，