题目内容
11.在平面直角坐标系中,点O为原点,平行于x轴的直线与抛物线L:y=ax2相交于A,B两点(点B在第一象限),点C在AB的延长线上.(1)已知a=1,点B的纵坐标为2.如图1,向右平移抛物线L使该抛物线过点B,与AB的延长线交于点C,AC的长为4$\sqrt{2}$.
(2)如图2,若BC=AB,过O,B,C三点的抛物线L3,顶点为P,开口向下,对应函数的二次项系数为a3,$\frac{{a}_{3}}{a}$=-$\frac{1}{3}$.
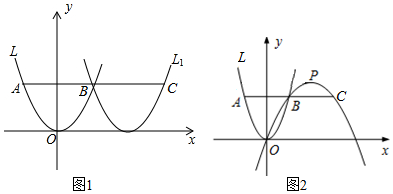
分析 (1)先确定抛物线L的解析式,根据点B的纵坐标为2,求出A和B的坐标,计算AB的长,利用对称性得出BC的长,所以AC=2AB=4$\sqrt{2}$;
(2)作辅助线:过B作BK⊥x轴于K,设OK=t,得出G(4t,0),设抛物线L3的解析式,并将B点的坐标代入可求得比值.
解答  解:(1)当a=1时,抛物线L的解析式为:y=x2,
解:(1)当a=1时,抛物线L的解析式为:y=x2,
当y=2时,2=x2,
∴x=±$\sqrt{2}$,
∵B在第一象限,
∴A(-$\sqrt{2}$,2),B($\sqrt{2}$,2),
∴AB=2$\sqrt{2}$,
∵向右平移抛物线L使该抛物线过点B,
∴AB=BC=2$\sqrt{2}$,
∴AC=4$\sqrt{2}$;
(2)如图2,设抛物线L3与x轴的交点为G,其对称轴与x轴交于Q,过B作BK⊥x轴于K,
设OK=t,则AB=BC=2t,
∴B(t,at2),
根据抛物线的对称性得:OQ=2t,OG=2OQ=4t,
∴O(0,0),G(4t,0),
设抛物线L3的解析式为:y=a3(x-0)(x-4t),
y=a3x(x-4t),
∵该抛物线过点B(t,at2),
∴at2=a3t(t-4t),
∵t≠0,
∴a=-3a3,
∴$\frac{{a}_{3}}{a}$=-$\frac{1}{3}$,
故答案为:(1)4$\sqrt{2}$;(2)-$\frac{1}{3}$.
点评 本题是二次函数图象与平移问题,考查了二次函数的性质和平移的原则及二次函数的轴对称性,解题的关键是理解题意,灵活运用待定系数法求函数的解析式.

练习册系列答案
 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
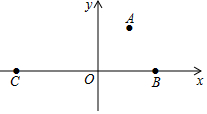
19. 如图,手掌盖住的点的坐标可能是( )
如图,手掌盖住的点的坐标可能是( )
 如图,手掌盖住的点的坐标可能是( )
如图,手掌盖住的点的坐标可能是( )| A. | (3,4) | B. | (-4,3) | C. | (-4,-3) | D. | (3,-4) |
6.下列计算正确的是( )
| A. | 3a-a=3 | B. | -2(x-4)=-2x+4 | C. | -(-32)=9 | D. | 4÷$\frac{5}{4}$×$\frac{4}{5}$=4÷1=4 |
 已知抛物线y=ax2+bx+2经过A(1,$\frac{5}{4}$),B(2,0)和C三个点.
已知抛物线y=ax2+bx+2经过A(1,$\frac{5}{4}$),B(2,0)和C三个点. 如图DF⊥AC于点F,BE⊥AC于点E,AB=CD,AF=CE.求证:BE=DF.
如图DF⊥AC于点F,BE⊥AC于点E,AB=CD,AF=CE.求证:BE=DF.