题目内容
6.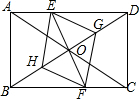 如图,在矩形ABCD中,点E在边AD上,点F在边BC上,且AE=CF,作EG∥FH,分别与对角线BD交于点G、H,连接EH、FG.
如图,在矩形ABCD中,点E在边AD上,点F在边BC上,且AE=CF,作EG∥FH,分别与对角线BD交于点G、H,连接EH、FG.(1)求证:△BFH≌△DEG;
(2)连接DF,若BF=DF,判断四边形EGFH是什么特殊四边形?并证明你的结论.
分析 (1)由平行四边形的性质得出AD∥BC,AD=BC,OB=OD,由平行线的性质得出∠FBH=∠EDG,∠OHF=∠OGE,得出∠BHF=∠DGE,求出BF=DE,由AAS即可得出结论;
(2)先证明四边形EGFH是平行四边形,再由等腰三角形的性质得出EF⊥GH,即可得出四边形EGFH是菱形.
解答 (1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,OB=OD,
∴∠FBH=∠EDG,
∵AE=CF,
∴BF=DE,
∵EG∥FH,
∴∠OHF=∠OGE,
∴∠BHF=∠DGE,
在△BFH和△DEG中,$\left\{\begin{array}{l}{∠FBH=∠EDG}&{\;}\\{∠BHF=∠DGE}&{\;}\\{BF=DE}&{\;}\end{array}\right.$,
∴BFH≌△DEG(AAS);
(2)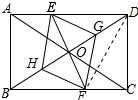 解:四边形EGFH是菱形;理由如下:
解:四边形EGFH是菱形;理由如下:
连接DF,如图所示:
由(1)得:BFH≌△DEG,
∴FH=EG,
又∵EG∥FH,
∴四边形EGFH是平行四边形,
∵BF=DF,OB=OD,
∴EF⊥BD,
∴EF⊥GH,
∴四边形EGFH是菱形.
点评 本题考查了全等三角形的性质和判定,平行线的性质,菱形的判定,等腰三角形的性质,平行四边形的性质和判定等知识;熟练掌握平行四边形的判定与性质,证明三角形全等是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.-$\frac{1}{2017}$的倒数的相反数是( )
| A. | $\frac{1}{2017}$ | B. | 2016 | C. | 2017 | D. | 2018 |
17.在一个不透明的口袋里装有若干个质地相同的红球,为了估计袋中红球的数量,某学习小组做了摸球实验,他们将30个与红球大小形状完全相同的白球装入袋中,搅匀后从中随机摸出一个球并记下颜色,再把它放回袋中,多次重复摸球.下表是多次活动汇总后统计的数据:
(1)请估计:当次数S很大时,摸到白球的频率将会接近0.3;假如你去摸一次,你摸到红球的概率是0.7(精确到0.1).
(2)试估算口袋中红球有多少只?
| 摸球的次数S | 150 | 200 | 500 | 900 | 1000 | 1200 |
| 摸到白球的频数n | 51 | 64 | 156 | 275 | 303 | 361 |
| 摸到白球的频率 | 0.34 | 0.32 | 0.312 | 0.306 | 0303 | 0.301 |
(2)试估算口袋中红球有多少只?
14.下列命题中,真命题的是( )
| A. | 对角线互相垂直的四边形是菱形 | |
| B. | 对角线互相垂直平分的四边形是正方形 | |
| C. | 对角线相等的四边形是矩形 | |
| D. | 对角线互相平分的四边形是平行四边形 |
1.下列汽车标志中,不是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
18.下列计算结果,正确的是( )
| A. | $\sqrt{(-5)^{2}}$=-5 | B. | $\sqrt{3}$×$\sqrt{4}$=$\sqrt{7}$ | C. | $\sqrt{12}$÷$\sqrt{3}$=2 | D. | (-$\sqrt{3}$)2=-3 |
 如图(1),图中的∠165°;
如图(1),图中的∠165°; 如图,一次函数y=-$\frac{1}{2}$x+m(m>0)的图象与x轴、y轴分别交于点A、B,点C在线段OA上,点C的横坐标为n,点D在线段AB上,且AD=2BD,将△ACD绕点D旋转180°后得到△A1C1D.
如图,一次函数y=-$\frac{1}{2}$x+m(m>0)的图象与x轴、y轴分别交于点A、B,点C在线段OA上,点C的横坐标为n,点D在线段AB上,且AD=2BD,将△ACD绕点D旋转180°后得到△A1C1D.