题目内容
如图,在平面直角坐标系中,直线l:y= x,直线l2:y=
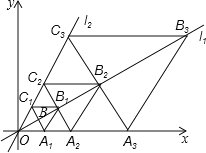
x,直线l2:y=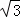 x,在直线l1上取一点B,使OB=1,以点B为对称中心,作点O的对称点B1,过点B1作B1A1∥l2,交x轴于点A1,作B1C1∥x轴,交直线l2于点C1,得到四边形OA1B1C1;再以点B1为对称中心,作O点的对称点B2,过点B2作B2A2∥l2,交x轴于点A2,作B2C2∥x轴,交直线l2于点C2,得到四边形OA2B2C2;…;按此规律作下去,则四边形OAnBnCn的面积是 .
x,在直线l1上取一点B,使OB=1,以点B为对称中心,作点O的对称点B1,过点B1作B1A1∥l2,交x轴于点A1,作B1C1∥x轴,交直线l2于点C1,得到四边形OA1B1C1;再以点B1为对称中心,作O点的对称点B2,过点B2作B2A2∥l2,交x轴于点A2,作B2C2∥x轴,交直线l2于点C2,得到四边形OA2B2C2;…;按此规律作下去,则四边形OAnBnCn的面积是 .

解:∵直线l:y= x,直线l2:y=
x,直线l2:y= x,
x,
∴直线l1与x轴夹角为30°,直线l2与x轴夹角为60°,B为l1上一点,且OB=1,
根据题意可知:OB=1,OB1=2,OB2=4,OB3=8,OB4=16,..OBn=2n,四边形OA1B1C1、四边形OA2B2C2、四边形OA3B3C3…是菱形,
∵∠A1OC1=60°,
∴△OA1C1,△OA2C2,△OAC,△OA3C3,…△OAnCn是等边三角形,
∴OA1=A1C1,OA2=A2C2,OA3=A3C3…OAn=AnCn,
∵OA1=A1C1= ,OA2=A2C2=
,OA2=A2C2= ,OA3=A3C3=
,OA3=A3C3= ,…OAn=AnCn=
,…OAn=AnCn=

∴四边形OAnBnCn的面积=AnCn•OBn=×
 ×2n=
×2n=
 .
.

练习册系列答案
相关题目
﹣ 的倒数是( )
的倒数是( )
|
| A. |
| B. | ﹣ | C. | ﹣5 | D. | 5 |
下列运算正确的是( )
|
| A. | a+a=a2 | B. | (﹣a3)4=a7 | C. | a3•a=a4 | D. | a10÷a5=a2 |



 ﹣
﹣ =0解是( )
=0解是( ) B. x=
B. x= C. x=
C. x= D. x=﹣1
D. x=﹣1
 ,用含x的代数式表示y得:y=__________.
,用含x的代数式表示y得:y=__________.