Question

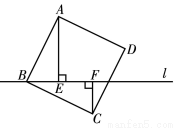
如图，CA、CB为⊙O的切线，切点分别为A、B．直径延长AD与CB的延长线交于点E．AB、CO交于点M，连接OB．

（1）求证：∠ABO=∠ACB；

（2）若sin∠EAB=，CB=12，求⊙O 的半径及的值．

 

 

Answer 1

（1）证明见解析；（2）4，．

【解析】

试题分析：（1）证明∠ABO =∠BCO即可证得∠ABO=∠ACB.

（2）由sin∠BCO =sin∠EAB=可求得＝，从而由CB＝12求得⊙O 的半径OB为4；由△OBE∽△CAE列比例式得＝．

（1）∵CA、CB为⊙O的切线，

∴ CA=CB， ∠BCO=∠ACB，∴∠CBO=90°．∴ CO⊥AB．

∴ ∠ABO +∠CBM=∠BCO +∠CBM=90°．∴ ∠ABO =∠BCO．∴ ∠ABO=∠ACB．

（2） ∵ OA＝OB， ∴∠EAB=∠ABO．∴ ∠BCO＝∠EAB．

∵ sin∠BCO =sin∠EAB=，∴ ＝．

∵ CB＝12，∴ OB＝4， 即⊙O 的半径为4．

∵∠OBE＝∠CAE＝90°，∠E＝∠E，∴△OBE∽△CAE．∴＝．

∵CA＝CB＝12，∴＝．

考点：1.切线的性质；2.等腰三角形的性质；3锐角三角函数定义；4.勾股定理；5.相似三角形的判定和性质.