题目内容
17.已知关于x的方程$\frac{x}{x-3}$-2=$\frac{m}{x-3}$有一个正整数解,则正整数m的可能取值共有4个.分析 先去分母,解得x=6-m(x≠3),根据关于x的方程$\frac{x}{x-3}$-2=$\frac{m}{x-3}$有一个正整数解,m=5,4,2,1,0.则正整数m的可能取值共有5个.
解答 解:去分母得:x-2(x-3)=m,
解得:x=6-m,
x-3≠0,
x≠3,
∵关于x的方程$\frac{x}{x-3}$-2=$\frac{m}{x-3}$有一个正整数解,
∴m=5,4,2,1.
则正整数m的可能取值共有4个,
故答案为:4.
点评 本题考查了分式方程的解,解决本题的关键是求出分式方程的解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
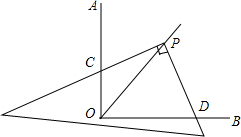 如图,∠AOB=90°,将直角三角尺的直角顶点P放在∠AOB的角平分线上,直角三角尺的两条直角边分别交OA于点C,交OB于点D,求证:PC=PD.
如图,∠AOB=90°,将直角三角尺的直角顶点P放在∠AOB的角平分线上,直角三角尺的两条直角边分别交OA于点C,交OB于点D,求证:PC=PD. 如图,试说明矩形ABCD的四个顶点在同一个圆上.
如图,试说明矩形ABCD的四个顶点在同一个圆上.