题目内容
 如图,AC切⊙O于点C,AB过圆心O交⊙O于点B、D,且AC=BC,
如图,AC切⊙O于点C,AB过圆心O交⊙O于点B、D,且AC=BC,(1)求∠A的度数;
(2)若⊙O的半径为2,求图中阴影部分的面积.
考点:切线的性质,扇形面积的计算
专题:
分析:(1)首先连接OC,由AC切⊙O于点C,可得OC⊥AC,然后设∠A=x°,由AB=AC以及圆周角定理,可得∠B=x°,∠AOC=2x°,继而求得答案;
(2)首先连接CD,易得△OCD是等边三角形.继而可由S阴影=S△ACO-S扇形ODC求得答案.
(2)首先连接CD,易得△OCD是等边三角形.继而可由S阴影=S△ACO-S扇形ODC求得答案.
解答:解:(1)连接OC.
∵AC切⊙O于点C,
∴OC⊥AC.
∴∠ACO=90°,
设∠A=x°,
∵AC=BC,
∴∠B=∠A=x°.
∵OB=OC,
∴∠OCB=∠B=x°.
∴∠AOC=∠OCB+∠B=2x°.
在Rt△ACO中,
∵∠A+∠AOC=90°,
∴x+2x=90.
∴x=30.
即∠A=30°.
 (2)连接DC.
(2)连接DC.
在Rt△ACO中,∠AOC=90°-∠A=60°.
又∵OD=OC,
∴△OCD是等边三角形.
∴CD=OD=2,∠AOC=60°.
∵BD是直径,
∴∠DCB=90°,BD=4.
由勾股定理得BC=2
.
∴AC=BC=2
.
∴S△ACO=
AC•OC=2
,
S扇形ODC=
π•22=
π,
∴S阴影=S△ACO-S扇形ODC=2
-
π.
∵AC切⊙O于点C,
∴OC⊥AC.
∴∠ACO=90°,
设∠A=x°,
∵AC=BC,
∴∠B=∠A=x°.
∵OB=OC,
∴∠OCB=∠B=x°.
∴∠AOC=∠OCB+∠B=2x°.
在Rt△ACO中,
∵∠A+∠AOC=90°,
∴x+2x=90.
∴x=30.
即∠A=30°.
 (2)连接DC.
(2)连接DC.在Rt△ACO中,∠AOC=90°-∠A=60°.
又∵OD=OC,
∴△OCD是等边三角形.
∴CD=OD=2,∠AOC=60°.
∵BD是直径,
∴∠DCB=90°,BD=4.
由勾股定理得BC=2
| 3 |
∴AC=BC=2
| 3 |
∴S△ACO=
| 1 |
| 2 |
| 3 |
S扇形ODC=
| 60 |
| 360 |
| 2 |
| 3 |
∴S阴影=S△ACO-S扇形ODC=2
| 3 |
| 2 |
| 3 |
点评:此题考查了切线的性质、圆周角定理、勾股定理以及扇形的面积.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想与方程思想的应用.

练习册系列答案
相关题目
 如图,图中共有三角形( )
如图,图中共有三角形( )| A、4个 | B、5个 | C、6个 | D、8个 |
在-
,π,-0.1010010001…,0,0.33
这五个数中,有理数的个数为( )
| 22 |
| 7 |
| • |
| 3 |
| A、1 | B、2 | C、3 | D、4 |
若|a|=5,|b|=1,且a-b<0,则a+b的值等于( )
| A、4或6 | B、4或-6 |
| C、-6或6 | D、-6或-4 |
下列数据不能确定物体位置的是( )
| A、6楼7号 |
| B、北偏东20° |
| C、龙华路25号 |
| D、东经118°、北纬40° |
反比例函数y=-
的图象过点(2,-m),则m的值是( )
| 4 |
| x |
| A、1 | B、2 | C、-2 | D、4 |
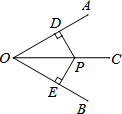 如图,∠AOC=∠BOC,点P在OC上,PD⊥OA于点D,PE⊥OB于点E,若OD=8,OP=10,则PE=
如图,∠AOC=∠BOC,点P在OC上,PD⊥OA于点D,PE⊥OB于点E,若OD=8,OP=10,则PE=