Question

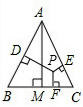
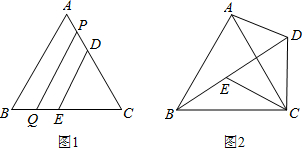
已知等边△ABC和Rt△DEF按如图所示的位置放置，点B，D重合，且点Ｅ、B(D)、
C在同一条直线上．其中∠E=90°, ,，现将△DEF
沿直线BC以每秒个单位向右平移，直至E点与C 点重合时停止运动，设运动时
间为t秒．
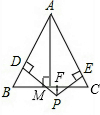
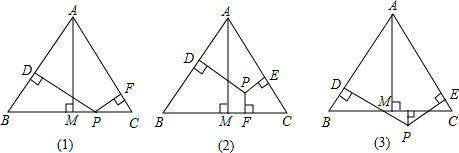
(1) 试求出在平移过程中，点F落在△ABC的边上时的t值；
(2) 试求出在平移过程中△ABC和Rt△DEF重叠部分的面积s与t的函数关系式；
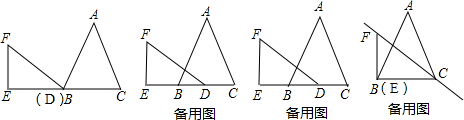
(3) 当D与C重合时，点H为直线DF上一动点，现将△DBH绕点D顺时针旋转60°得到       
△ACK，则是否存在点H使得△BHK的面积为，若存在，试求出CH的值；若不存在，请说明理由．

Answer 1

（1）．



∴．…………………………………2分
又FN＝FM+MN    ∵BM＝FM·sin30⁰=，
∴AM==MN．
∴FN=．
∴.………………………………4分
∴当₁=8,₂=10时，点F落在△ABC的边上．
（2）当， ． ………5分当 ，  
              ……………………………6分
当≤10，

……………………7分
当≤，

．…………………………………………………………………8分

（3）①当点H在EC的上方，且在BK左侧时

……………………………………………………10分
②当点H在EC的上方，且在BK右侧时

∴无解，所以，此时不存在点H．………………11分
③点H在EC下方时
                                                                             
∴…………………………………………………………………………………12分
综上所述：．

解析