Question

已知等边△ABC和点P，设点P到△ABC三边的AB、AC、BC的距离分别是h₁，h₂，h₃，△ABC的高为h，请你探索以下问题：
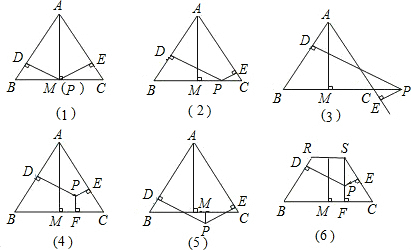
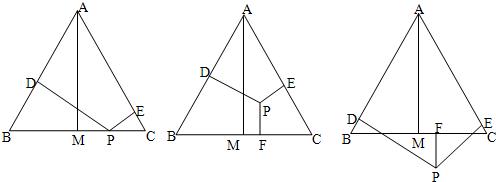
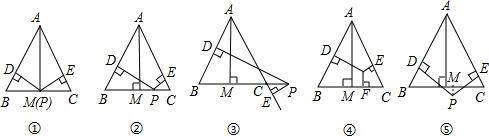
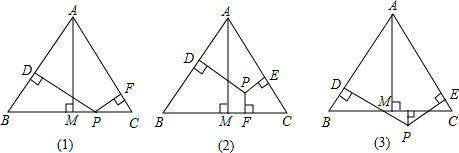
（1）若点P在一边BC上（图1），此时h₃=0，问h₁、h₂与h之间有怎样的数量关系？请说明理由；
（2）若当点P在△ABC内（图2），此时h₁、h₂、h₃与h之间有怎样的数量关系？请说明理由；
（3）若点P在△ABC外（图3），此时h₁、h₂、h₃与h之间有怎样的数量关系

h=h₁+h₂-h₃

．（请直接写出你的猜想，不需要说明理由．）

Answer 1

分析：把点P与各顶点分别连接起来．根据组合图形的面积与分割成的图形面积之间的关系建立关系式，然后根据等边三角形性质求解．

解答：解：
（1）h=h₁+h₂，理由如下：
连接AP，则 S_△ABC=S_△ABP+S_△APC
∴

1

2

BC•AM=

1

2

AB•PD+

1

2

AC•PF
即

1

2

BC•h=

1

2

AB•h₁+

1

2

AC•h₂
又∵△ABC是等边三角形
∴BC=AB=AC，
∴h=h₁+h₂．

（2）h=h₁+h₂+h₃ ，理由如下：
连接AP、BP、CP，则 S_△ABC=S_△ABP+S_△BPC+S_△ACP
∴

1

2

BC•AM=

1

2

AB•PD+

1

2

AC•PF+

1

2

BC•PE
即

1

2

BC•h=

1

2

AB•h₁+

1

2

AC•h₂₊

1

2

BC•h₃
又∵△ABC是等边三角形，
∴BC=AB=AC．
∴h=h₁+h₂+h₃．

（3）h=h₁+h₂-h₃．
当点P在△ABC外时，结论h₁+h₂+h₃=h不成立．此时，它们的关系是h₁+h₂-h₃=h．
理由如下：连接PB，PC，PA
由三角形的面积公式得：S_△ABC=S_△PAB+S_△PAC-S_△PBC，
即

1

2

BC•AM=

1

2

AB•PD+

1

2

AC•PE-

1

2

BC•PF，
∵AB=BC=AC，
∴h₁+h₂-h₃=h，
即h₁+h₂-h₃=h．

点评：此题考查等边三角形的性质，运用等积法建立关系构思巧妙，也是此题的难点．