题目内容
已知等边△ABC和三角形内一点P,设点P到△ABC三边的距离分别为h1、h2、h3,△ABC的高为h.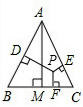
(1)请写出h与h1、h2、h3的关系式,并说明理由;
(2)若点P在等边△ABC的边上,仍有上述关系吗?
(3)若点P在三角形外,仍有上述关系吗?若有,请你证明,若没有,请你写出它们新的关系式,并给予证明.
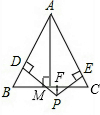
分析:(1)连接PA,PB,PC,由S△ABC=S△PAC+S△PBC+S△PAB,可得
BC•h=
AB•h1+
AC•h2+
BC•h3,又由△ABC是等边三角形,即可得h=h1+h2+h3;
(2)利用(1)的证明方法,可从P在AC上,则h2=0,去分析,仍可求得h=h1+h2+h3;
(3)连接PA,PB,PC,则可得S△ABC=S△PAC+S△PBC-S△PAB,然后利用(1)中的分析方法,即可求得h=h1+h2-h3.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(2)利用(1)的证明方法,可从P在AC上,则h2=0,去分析,仍可求得h=h1+h2+h3;
(3)连接PA,PB,PC,则可得S△ABC=S△PAC+S△PBC-S△PAB,然后利用(1)中的分析方法,即可求得h=h1+h2-h3.
解答: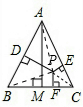 解:(1)连接PA,PB,PC,
解:(1)连接PA,PB,PC,
则S△ABC=S△PAC+S△PBC+S△PAB,
∴
BC•h=
AB•h1+
AC•h2+
BC•h3,
∵△ABC是等边三角形,
∴AB=BC=AC,
∴h=h1+h2+h3;
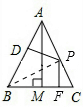 (2)仍有h=h1+h2+h3;
(2)仍有h=h1+h2+h3;
理由:如图:设P在AC上,则h2=0,
连接PB,
则S△ABC=S△PBC+S△PAB,
∴
BC•h=
AB•h1+
BC•h3,
∵△ABC是等边三角形,
AB=BC=AC,
∴h=h1+h3;
即h=h1+h2+h3;
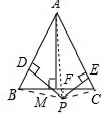 (3)h=h1+h2-h3.
(3)h=h1+h2-h3.
连接PA,PB,PC,
则S△ABC=S△PAC+S△PBC-S△PAB,
∴
BC•h=
AB•h1+
AC•h2-
BC•h3,
∵△ABC是等边三角形,
∴AB=BC=AC,
∴h=h1+h2-h3.
 解:(1)连接PA,PB,PC,
解:(1)连接PA,PB,PC,则S△ABC=S△PAC+S△PBC+S△PAB,
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵△ABC是等边三角形,
∴AB=BC=AC,
∴h=h1+h2+h3;
 (2)仍有h=h1+h2+h3;
(2)仍有h=h1+h2+h3;理由:如图:设P在AC上,则h2=0,
连接PB,
则S△ABC=S△PBC+S△PAB,
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵△ABC是等边三角形,
AB=BC=AC,
∴h=h1+h3;
即h=h1+h2+h3;
 (3)h=h1+h2-h3.
(3)h=h1+h2-h3.连接PA,PB,PC,
则S△ABC=S△PAC+S△PBC-S△PAB,
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵△ABC是等边三角形,
∴AB=BC=AC,
∴h=h1+h2-h3.
点评:此题考查了等边三角形的性质与三角形面积的求解方法.此题难度适中,解题的关键是注意数形结合思想的应用,注意辅助线的作法.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
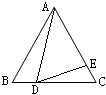
 23、如图,已知等边三角形ABC,在AB上取点D,在AC上取点E,使得AD=AE,作等边三角形PCD,QAE和RAB,求证:P、Q、R是等边三角形的三个顶点.
23、如图,已知等边三角形ABC,在AB上取点D,在AC上取点E,使得AD=AE,作等边三角形PCD,QAE和RAB,求证:P、Q、R是等边三角形的三个顶点.
 已知等边△ABC边长为4,D、E分别为BC和AC上的点,且△ABD∽△DCE,则∠ADE=
已知等边△ABC边长为4,D、E分别为BC和AC上的点,且△ABD∽△DCE,则∠ADE= 已知等边△ABC边长为4,D、E分别为BC和AC上的点,且△ABD∽△DCE,则∠ADE=________度;若点D为BC的三等分点,则EC=________.
已知等边△ABC边长为4,D、E分别为BC和AC上的点,且△ABD∽△DCE,则∠ADE=________度;若点D为BC的三等分点,则EC=________.