��Ŀ����
15�� ��֪��������������֧ͼ�����ԭ��Գƣ�������һ���۽⼯�������⣺��ͼ����ͬһֱ������ϵ�У�����������y=kx��ͼ���뷴��������y=$\frac{\sqrt{3}}{x}$��ͼ��ֱ��ڵ�һ�������ĵ�B��D����֪��A��-m��0����C��m��0����
��֪��������������֧ͼ�����ԭ��Գƣ�������һ���۽⼯�������⣺��ͼ����ͬһֱ������ϵ�У�����������y=kx��ͼ���뷴��������y=$\frac{\sqrt{3}}{x}$��ͼ��ֱ��ڵ�һ�������ĵ�B��D����֪��A��-m��0����C��m��0������1����գ�����kֵȡ��ֵʱ���ı���ABCD����״һ����ƽ���ı��Σ�
��2���ٵ�m=2����B����Ϊ��p��1��ʱ���ı���ABCD����״һ���Ǿ��Σ�
����գ��Ԣ��е�mֵ����ʹ�ı���ABCDΪ���εĵ�B����2����
��3���ı���ABCD�ܲ��������Σ����ܣ�ֱ��д��B������ꣻ�����ܣ�˵�����ɣ�
���� ��1�����ݶԳƵ����ʿɵ��ı���ABCD�ĶԽ�����ƽ�֣���һ����ƽ���ı��Σ�
��2���ٰ�B��������뷴���������Ľ���ʽ�������p��ֵ�����ô���ϵ�������k��ֵ�����ù��ɶ������OB��ֵ���Ӷ��ó�OA=OB=OC���ó���ABC=90�㣻
�ڸ��ݷ���������ͼ��ĶԳ��ԣ��ڷ���������ͼ���ϣ����߾���O�������ߵ���AC��һ�������飬�ݴ˼����жϣ�
��3�������ı���ABCD�ĶԽ���һ�����ܴ�ֱ�����жϣ�
��� �⣺��1�����ݶԳ��Կɵã�OB=OD��
��A��-m��0����C��m��0����
��OA=OC
���ı���ABCD��ƽ���ı��Σ�
�ʴ��ǣ�ƽ���ı��Σ�
��2���١ߵ�B��p��1����y=$\frac{\sqrt{3}}{x}$�ϣ�
��1=$\frac{\sqrt{3}}{p}$�����p=$\sqrt{3}$��B��$\sqrt{3}$��1������y=kx��k=$\frac{\sqrt{3}}{3}$��
��OB2=��$\sqrt{3}$��2+12=4��
��OB=2��
��m=2��
��OA=OC=2��
��OA=OB=OC=2��
���ABC=90�㣬
�ɣ�1���У��ı���ABCD��ƽ���ı��Σ�
��ƽ���ı���ABCD�Ǿ��Σ�
�ʴ�Ϊ���Σ�
�� �ɢٵã�m=2��
�ɢٵã�m=2��
��ͼ��������һ�������Ľǵ�ƽ���ߣ�������������ͼ���ڵ�M��N����MN�Ľ���ʽ��y=x��
��x=m=2ʱ�������������϶�Ӧ�ĵ��ǣ�2��$\frac{\sqrt{3}}{2}$����ֱ��y=x�϶�Ӧ�ĵ��ǣ�2��2����
��2��$\frac{\sqrt{3}}{2}$
�ࣨ2��$\frac{\sqrt{3}}{2}$����OM���ӳ����ϣ���MN��AC��
����ʹ�ı���ABCD�Ǿ��εĵ�B����2����
�ʴ��ǣ�2��
��3���ı���ABCD���������Σ�
�����ǣ���A��-m��0����C��m��0����
���ı���ABCD�ĶԽ���AC��x���ϣ�
�֡ߵ�B��D�ֱ��������������뷴���������ڵ�һ�������Ľ��㣬
��Խ���BD��AC�����ܴ�ֱ��
���ı���ABCD�����������Σ�
���� ���⿼���˷�����������ͼ��ĶԳ����Լ����ε��ж�����ȷ���������������뷴������������ԭ��Գ��ǹؼ���

| ���� | 83 | 76 | 88 | 82 | 85 | 90 |
| �Ż� | 79 | 81 | 91 | 74 | 90 | 89 |
��2����������ͳ�Ƶ�֪ʶ��˵����λͬѧ�ijɼ��Ƚ��ȶ���
| A�� | 2 | B�� | 3 | C�� | -2 | D�� | -3 |
 ��ͼ��ƽ��ֱ������ϵ����������OABC����A������Ϊ��1��2�������C������Ϊ��������
��ͼ��ƽ��ֱ������ϵ����������OABC����A������Ϊ��1��2�������C������Ϊ��������| A�� | ��-3��1�� | B�� | ��-2��1�� | C�� | ��2��-1�� | D�� | ��-2��0.5�� |
 ��ͼ�������ǰ��ֱ�Ƕ������ֱ�ߵ�һ���ϣ�����1=30�㣬���2=60�㣮
��ͼ�������ǰ��ֱ�Ƕ������ֱ�ߵ�һ���ϣ�����1=30�㣬���2=60�㣮 ��ͼ��ƽ���ı���ABCD�ĶԽ���AC=6cm����ƽ���ı���ABCD����Գ�������ת180�㣬��C����ת����·������
��ͼ��ƽ���ı���ABCD�ĶԽ���AC=6cm����ƽ���ı���ABCD����Գ�������ת180�㣬��C����ת����·������ ��ͼ��ijУ����ѧ����ѧ��ʽ��һ�γ��������������Ƴ�һ��δ��ɵ�����ͳ��ͼ�����˳���ѧ����150�ˣ���ݴ˹��Ʋ��е���400�ˣ�
��ͼ��ijУ����ѧ����ѧ��ʽ��һ�γ��������������Ƴ�һ��δ��ɵ�����ͳ��ͼ�����˳���ѧ����150�ˣ���ݴ˹��Ʋ��е���400�ˣ�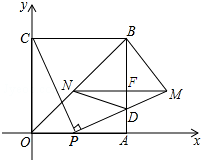 ��ͼ���ı���OABC�DZ߳�Ϊ4�������Σ���PΪOA��������һ�㣨���O��A���غϣ�������CP������P��PM��CP��AB�ڵ�D����PM=CP������M��MN��AO����BO�ڵ�N������ND��BM����OP=t��
��ͼ���ı���OABC�DZ߳�Ϊ4�������Σ���PΪOA��������һ�㣨���O��A���غϣ�������CP������P��PM��CP��AB�ڵ�D����PM=CP������M��MN��AO����BO�ڵ�N������ND��BM����OP=t��