题目内容
11.(1)若干名学生分宿舍,每间4人余20人,每间8人,其中一间不空也不满,则宿舍有6间,学生有44人.(2)若干名学生分宿舍,每间4人余20人,每间8人,则有一个房间还有空位,学校可能有几间房?可安排多少学生住宿?
分析 (1)先设宿舍有x间,则总人数是(4x+20)人,最后一间的人数是4x+20-8(x-1),再根据有一间不空也不满列出不等式组,解出x的取值范围,即可得出答案;
(2)设有x间住房,有y名学生住宿.根据“每间住4人,余20人;如果每间住8人,那么有一间房还有位”作为关系式,从而求出x的值,把符合题意的y值代入即可.
解答 解:(1)设宿舍有x间,根据题意得:
$\left\{\begin{array}{l}{4x+20-8(x-1)>0}\\{4x+20-8(x-1)<8}\end{array}\right.$,
解得:5<x<7,
∵x为正整数,
∴x=6,
则宿舍有6间,学生有:4×6+20=44(人),
故答案为:6,44.
(2)设有x间住房,有y名学生住宿,
则有y=4x+20,
根据题意得:$\left\{\begin{array}{l}{8x-(4x+20)>0}\\{8x-(4x+20)<8}\end{array}\right.$,
解得:5<x<7,
因为x为整数,
所以x可取6,
把x的值代入y=4x+20得:y的值为44.
答:该校可能有6间住房,住宿学生有44人.
点评 本题考查一元一次不等式组的应用,将现实生活中的事件与数学思想联系起来,读懂题列出关系式即可求解.注意本题的不等关系为:每间住5人,那么有12人安排不下;如果每间住8人,那么有一间房还余一些床位.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.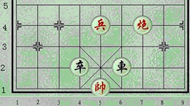 如图,若車的位置是(5,1),那么兵的位置可以记作( )
如图,若車的位置是(5,1),那么兵的位置可以记作( )
 如图,若車的位置是(5,1),那么兵的位置可以记作( )
如图,若車的位置是(5,1),那么兵的位置可以记作( )| A. | (1,5) | B. | (4,3) | C. | (3,4) | D. | (3,3) |
2.某乡镇对公路进行补修,甲工程队计划用若干天完成此项目,甲工程队单独工作了3天后,为缩短完成的时间,乙工程队加入此项目,且甲、乙工程队每天补修的工作量相同,结果提前3天完成,则甲工程队计划完成此项目的天数是( )
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
20.已知在Rt△ABC中,∠C=90°,c=5,两直角边a,b关于x的一元二次方程x2-mx+2m-2=0的两个根,则Rt△ABC中较小的锐角的正弦值为( )
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |