Question

【题目】如图，已知，、的交点为，现作如下操作：

第一次操作，分别作和的平分线，交点为，

第二次操作，分别作和的平分线，交点为，

第三次操作，分别作和的平分线，交点为，

…

第次操作，分别作和的平分线，交点为．

若度，那等于__________度．

Answer 1

【答案】

【解析】

先过E作EF∥AB，根据AB∥CD，得出AB∥EF∥CD，再根据平行线的性质，得出∠B=∠1，∠C=∠2，进而得到∠BEC=∠ABE+∠DCE；根据∠ABE和∠DCE的平分线交点为E1，则可得出∠CE1B=∠ABE1+∠DCE1∠ABE∠DCE∠BEC；同理可得∠BE2C=∠ABE2+∠DCE2∠ABE1∠DCE1∠CE1B∠BEC；根据∠ABE2和∠DCE2的平分线，交点为E3，得出∠BE3C∠BEC；…据此得到规律∠En∠BEC，最后求得∠BEC的度数．

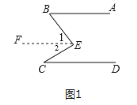
如图1，过E作EF∥AB．

∵AB∥CD，

∴AB∥EF∥CD，

∴∠B=∠1，∠C=∠2．

∵∠BEC=∠1+∠2，

∴∠BEC=∠ABE+∠DCE；

如图2．

∵∠ABE和∠DCE的平分线交点为E1，

∴∠CE1B=∠ABE1+∠DCE1∠ABE∠DCE∠BEC．

∵∠ABE1和∠DCE1的平分线交点为E2，

∴∠BE2C=∠ABE2+∠DCE2∠ABE1∠DCE1∠CE1B∠BEC；

∵∠ABE2和∠DCE2的平分线，交点为E3，

∴∠BE3C=∠ABE3+∠DCE3∠ABE2∠DCE2∠CE2B∠BEC；

…

以此类推，∠En∠BEC，

∴当∠En=1度时，∠BEC等于2n度．

故答案为：2n．