题目内容
 18、如图,以原点O为圆心的圆交x轴于A、B两点,交y轴的正半轴于点C,D为第一象限内⊙O上的一点,若∠DAB=20°,则∠OCD=
18、如图,以原点O为圆心的圆交x轴于A、B两点,交y轴的正半轴于点C,D为第一象限内⊙O上的一点,若∠DAB=20°,则∠OCD=65
°.分析:根据∠DAB=20°,得出∠DOB的度数,再利用等腰三角形的性质得出∠OCD=∠CDO,进而求出答案.
解答: 解:连接DO,∵∠DAB=20°,
解:连接DO,∵∠DAB=20°,
∴∠DOB=40°,
∴∠COD=90°-40°=50°,
∵CO=DO,
∴∠OCD=∠CDO,
∴∠OCD=(180°-50°)÷2=65°.
故答案为:65.
 解:连接DO,∵∠DAB=20°,
解:连接DO,∵∠DAB=20°,∴∠DOB=40°,
∴∠COD=90°-40°=50°,
∵CO=DO,
∴∠OCD=∠CDO,
∴∠OCD=(180°-50°)÷2=65°.
故答案为:65.
点评:此题主要考查了圆周角定理以及等腰三角形的性质,得出∠OCD=∠CDO是解决问题的关键.

练习册系列答案
相关题目
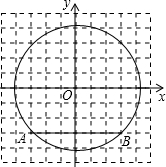 如图,以原点O为圆心作一个半径为
如图,以原点O为圆心作一个半径为 如图,以原点O为圆心的圆交x轴于A,B两点,交y轴的正半轴于点C,D为第一象限内⊙O上的一点,若∠DAB=30°,则∠OCD=
如图,以原点O为圆心的圆交x轴于A,B两点,交y轴的正半轴于点C,D为第一象限内⊙O上的一点,若∠DAB=30°,则∠OCD=