题目内容
7.已知?ABCD中,AB=13,AC=24,BD=10,则?ABCD的面积是120.分析 只要证明四边形ABCD是菱形即可解决问题.
解答 解:如图,
∵四边形ABCD是平行四边形,
∴OA=OC=12,OD=OB=5,
∵AD=13,
∴AD2=OD2+OA2,
∴∠AOD=90°,
∴AC⊥BD,
∴四边形ABCD是菱形,
∴S四边形ABCD=$\frac{1}{2}$•AC•BD=120,
故答案为120.
点评 本题考查平行四边形的性质、菱形的判定、勾股定理的逆定理等知识,解题的关键是灵活运用所学知识解决问题,本题体现了数形结合的思想,属于中考常考题型.

练习册系列答案
 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
12.下列说法中正确的个数是( )
①两个三角形中,有两条边对应相等,则可以用“HL”来判定这两个三角形全等;
②有一条直角边和一个锐角对应相等的两个三角形全等;
③有两条直角边分别相等的两个直角三角形全等;
④两锐角对应相等的两个直角三角形全等.
①两个三角形中,有两条边对应相等,则可以用“HL”来判定这两个三角形全等;
②有一条直角边和一个锐角对应相等的两个三角形全等;
③有两条直角边分别相等的两个直角三角形全等;
④两锐角对应相等的两个直角三角形全等.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
19. 如图,∠1=25°,则射线OA表示为( )
如图,∠1=25°,则射线OA表示为( )
 如图,∠1=25°,则射线OA表示为( )
如图,∠1=25°,则射线OA表示为( )| A. | 南偏西65° | B. | 南偏西25° | C. | 南偏东65° | D. | 南偏东25°. |
16.某班45名同学在一次数学测验中,25名男生的平均得分为m,20名女生的平均得分为n,这个班的所有同学的平均得分是( )
| A. | $\frac{m+n}{25}$ | B. | $\frac{25m+20n}{45}$ | C. | $\frac{m+n}{2}$ | D. | $\frac{20(m+n)}{45}$ |
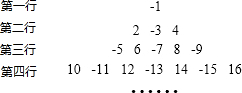 将有理数-1,2,-3,4,-5,6,-7,…排成如图的形式(下一行比上一行多两个数),观察各行右边的数的规律,按此规律推算第10行从左边数第4个数是-85.
将有理数-1,2,-3,4,-5,6,-7,…排成如图的形式(下一行比上一行多两个数),观察各行右边的数的规律,按此规律推算第10行从左边数第4个数是-85. 在直线l上顺次取A、B、C三点,使得AB=6cm,BC=10cm,若点D是线段AC的中点,则线段BD=2cm.
在直线l上顺次取A、B、C三点,使得AB=6cm,BC=10cm,若点D是线段AC的中点,则线段BD=2cm.