题目内容
如图,AB为⊙O的直径,PD切⊙O于点C,交AB的延长线于点D,且∠D=2∠CAD.
(1)求∠D的度数;
(2)若CD=2,求BD的长.



解:(1)∵OA=OC,
∴∠A=∠ACO,
∴∠COD=∠A+∠ACO=2∠A,
∵∠D=2∠CAD,
∴∠D=∠COD,
∵PD切⊙O于C,
∴∠OCD=90°,
∴∠D=∠COD=45°;
(2)∵∠D=∠COD,CD=2,
∴OC=OB=CD=2,
在Rt△OCD中,由勾股定理得: 22+22=(2+BD)2,
22+22=(2+BD)2,
解得:BD=2 ﹣2.
﹣2.



练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
今年5月10日,在市委宣传部、市教育局等单位联合举办的“走复兴路,圆中国梦”中学生演讲比赛中,7位评委给参赛选手张阳同学的打分如表:
| 评委代号 | A | B | C | D | E | F | G |
| 评分 | 90 | 92 | 86 | 92 | 90 | 95 | 92 |
则张阳同学得分的众数为( )
|
| A. | 95 | B. | 92 | C. | 90 | D. | 86 |



 将随意地落在如图所示的方格地面上,每个小方格形状完全相同,则小鸟落在阴影方格地面上的概率是 .
将随意地落在如图所示的方格地面上,每个小方格形状完全相同,则小鸟落在阴影方格地面上的概率是 .
 +|﹣1|﹣(
+|﹣1|﹣( ﹣1)0
﹣1)0 =
= .
. 的整数解共有( )
的整数解共有( ) 0°.
0°.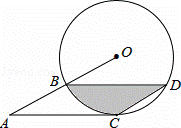
 的图象相交于A(4,2)、B(﹣2,m)两点,则一次函数的表达式为
的图象相交于A(4,2)、B(﹣2,m)两点,则一次函数的表达式为