题目内容
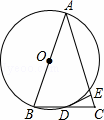
如图,点B、C、D都在半径为6的⊙O上,过点C作AC∥BD交OB的延长线于点A,连接CD,已知∠CDB=∠OBD=3 0°.
0°.
(1)求证:AC是⊙O的切线;
(2)求弦BD的长;
(3)求图中阴影部分的面积.
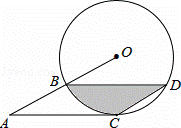
(1)证明:连接OC,OC交BD于E,
∵∠CDB=30°,
∴∠COB=2∠CDB=60°,
∵∠CDB=∠OBD,
∴CD∥AB,
又∵AC∥BD,
∴四边形ABDC为平行四边形,
∴∠A=∠D=30°,
∴∠OCA=180°﹣∠A﹣∠COB=90°,即OC⊥AC
又∵OC是⊙O的半径,
∴AC是⊙O的切线;
(2)解:由(1)知,OC⊥AC.
∵AC∥BD,
∴OC⊥BD,
∴BE=DE,
∵在直角△BEO中,∠OBD=30°,OB=6,
∴BE=OBcos30°=3 ,
,
∴BD=2BE=6 ;
;
(3)解:易证△OEB≌△CED,
∴S阴影=S扇形BOC
∴S阴影= =6π.
=6π.
答:阴影部分的面积是6π.


练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
某中学随机调查了15名学生,了解他们一周在校参加体育锻炼时间,列表如下:
| 锻炼时间(小时) | 5 | 6 | 7 | 8 |
| 人数 | 2 | 6 | 5 | 2 |
则这15名同学一周在校参加体育锻炼时间的中位数和众数分别是( )
|
| A. | 6,7 | B. | 7,7 | C. | 7,6 | D. | 6,6 |


作业时间是中小学教育质量综合评价指标的考查要点之一,腾飞学习小组五个同学每天课外作业时间分别是(单位:分钟):60,80,75,45,120.这组数据的中位数是( )
|
| A. | 45 | B. | 75 | C. | 80 | D. | 60 |
要使分式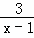 有意义,则的取值范围是( )
有意义,则的取值范围是( )
|
| A. | x≠1 | B. | x>1 | C. | x<1 | D. | x≠﹣1 |
如图是由4个相同的小正方形搭成的一个几何体,则它的俯视图是( )

|
| A. |
| B. |
| C. |
| D. |
|







 ,求CE的长.
,求CE的长.