题目内容
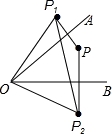
已知∠AOB=30°,点P在∠AOB内部,点P1与点P关于OA对称,点P2与点P关于OB对称,则△P1OP2是( )
A.含30°角的直角三角形 B.顶角是30°的等腰三角形
C.等边三角形 D.等腰直角三角形
C【考点】轴对称的性质.
【专题】证明题.
【分析】根据轴对称的性质,结合等边三角形的判定求解.
【解答】解:∵P为∠AOB内部一点,点P关于OA、OB的对称点分别为P1、P2,
∴OP=OP1=OP2且∠P1OP2=2∠AOB=60°,
∴故△P1OP2是等边三角形.
故选C.
【点评】本题考查轴对称的性质,对应点的连线与对称轴的位置关系是互相垂直,对应点所连的线段被对称轴垂直平分,对称轴上的任何一点到两个对应点之间的距离相等,对应的角、线段都相等.

练习册系列答案
相关题目
 的结果是( )
的结果是( ) 每天各能铺设多少米?
每天各能铺设多少米?
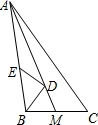
 点P的个数为( )
点P的个数为( )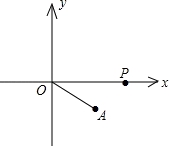
 B.
B. C.
C. D.
D.