题目内容
17.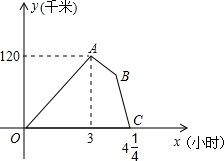 某物流公司的快递车和货车同时从甲地出发,以各自的速度匀速向乙地行驶,快递车到达乙地后卸完物品再另装货物共用45分钟,立即按原路以另一速度匀速返回,直至与货车相遇.已知货车的速度为60千米/时,两车之间的距离y(千米)与货车行驶时间x(小时)之间的函数图象如图所示.
某物流公司的快递车和货车同时从甲地出发,以各自的速度匀速向乙地行驶,快递车到达乙地后卸完物品再另装货物共用45分钟,立即按原路以另一速度匀速返回,直至与货车相遇.已知货车的速度为60千米/时,两车之间的距离y(千米)与货车行驶时间x(小时)之间的函数图象如图所示.(1)求甲、乙两地之间的距离是多少?
(2)求快递车返回时距离货车有多远?
(3)求快递车从乙地返回甲地的速度.
分析 (1)设快递车从甲地到乙地的速度为x千米/时,根据3小时相距120千米即可列方程求解;
(2)根据条件AB段所用的时间是45分钟,利用甲和乙之间的距离减去货车行驶的距离即可;
(3)求得B点对应的横坐标,设快递车从乙地返回甲地的速度是y千米/小时,根据距离公式即可列方程求解.
解答 解:(1)设快递车从甲地到乙地的速度为x千米/时,则
3(x-60)=120,
x=100.
则甲、乙两地之间的距离是3×100=300(千米);
(2)快递车返回时距离货车的距离是:300-60(3+$\frac{45}{60}$)=75(千米);
(3)设快递车从乙地返回甲地的速度是y千米/小时.
根据题意得:(60+y)【4$\frac{1}{4}$-(3+$\frac{45}{60}$)】=75,
解得:y=90.
则快递车从乙地返回甲地的速度是90千米/小时.
点评 本题考查的是用一次函数解决实际问题,此类题是近年中考中的热点问题,关键是根据一次函数的性质和图象结合实际问题判断出每一结论是否正确.

练习册系列答案
相关题目
8. 如图,若O为EH的中点,要使△EOF≌△HOG,不能加什么条件( )
如图,若O为EH的中点,要使△EOF≌△HOG,不能加什么条件( )
 如图,若O为EH的中点,要使△EOF≌△HOG,不能加什么条件( )
如图,若O为EH的中点,要使△EOF≌△HOG,不能加什么条件( )| A. | FO=GO | B. | AB∥CD | C. | ∠AFG=∠FGD | D. | EF=GH |
6.下面调查中,适合采用普查的事件是( )
| A. | 对全国中学生心理健康现状的调查 | |
| B. | 对我市食品合格情况的调查 | |
| C. | 对江苏卫视《最强大脑》收视率的调查 | |
| D. | 对你所在班级同学身高情况的调查 |
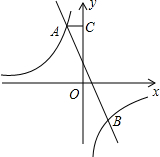 如图,已知双曲线y=$\frac{k}{x}$和直线y=mx+n交于点A和B,B点的坐标是(2,-3),AC垂直y轴于点C,AC=$\frac{3}{2}$;
如图,已知双曲线y=$\frac{k}{x}$和直线y=mx+n交于点A和B,B点的坐标是(2,-3),AC垂直y轴于点C,AC=$\frac{3}{2}$;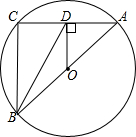 如图,AB是⊙O的直径,AC是⊙O的弦,作0D⊥AC,垂足为点D,连接BD.若AB=5cm,AC=4cm,则BD的长为$\sqrt{13}$.
如图,AB是⊙O的直径,AC是⊙O的弦,作0D⊥AC,垂足为点D,连接BD.若AB=5cm,AC=4cm,则BD的长为$\sqrt{13}$.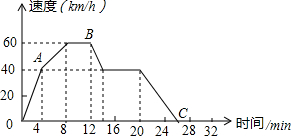 如图,根据汽车行驶情况的图象回答下列问题:
如图,根据汽车行驶情况的图象回答下列问题: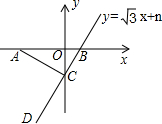 如图,点A的坐标为(-4,0),直线y=$\sqrt{3}$x+n与坐标轴交于点B、C,连接AC,如果∠ACD=90°,则n的值为$-\frac{4\sqrt{3}}{3}$.
如图,点A的坐标为(-4,0),直线y=$\sqrt{3}$x+n与坐标轴交于点B、C,连接AC,如果∠ACD=90°,则n的值为$-\frac{4\sqrt{3}}{3}$.