题目内容
在平面直角坐标系中,点A的坐标为(-6,6),以A为顶点的∠BAC的两边始终与x轴交于B、C两点(B在C左面),且∠BAC=45°.
(1)如图1,连接OA,当AB=AC时,试说明:OA=OB.
(2)过点A作AD⊥x轴,垂足为D,当DC=2时,将∠BAC沿AC所在直线翻折,翻折后边AB交y轴于点M,求点M的坐标.
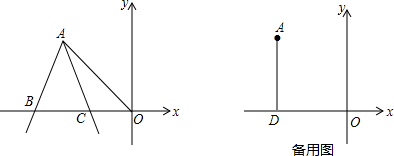
(1)如图1,连接OA,当AB=AC时,试说明:OA=OB.
(2)过点A作AD⊥x轴,垂足为D,当DC=2时,将∠BAC沿AC所在直线翻折,翻折后边AB交y轴于点M,求点M的坐标.
考点:全等三角形的判定与性质,坐标与图形性质,勾股定理,翻折变换(折叠问题)
专题:
分析:(1)利用等腰三角形的性质求得∠BAO和∠ABC的读数,然后利用等校对等边即可证得;
(2)当点C在点D右侧时,连接CM,过点A作AF⊥y轴于点F,证明△BAD≌△MAF,在Rt△COM中,由勾股定理即可求得M的横坐标;
当点C在点D左侧时,连接CM,过点A作AF⊥y轴于点F,证明△BAD≌△MAF,同理,在Rt△COM中,由勾股定理即可求得M的横坐标.
(2)当点C在点D右侧时,连接CM,过点A作AF⊥y轴于点F,证明△BAD≌△MAF,在Rt△COM中,由勾股定理即可求得M的横坐标;
当点C在点D左侧时,连接CM,过点A作AF⊥y轴于点F,证明△BAD≌△MAF,同理,在Rt△COM中,由勾股定理即可求得M的横坐标.
解答: 解:(1)∵AB=AC,∠BAC=45°,
解:(1)∵AB=AC,∠BAC=45°,
∴∠ABC=∠ACB=67.5°.
过点A作AE⊥OB于E,
则△AEO是等腰直角三角形,∠EAO=45°.
∵AB=AC,AE⊥OB,
∴∠BAE=
∠BAC=22.5°.
∴∠BAO=67.5°=∠ABC,
∴OA=OB.
(2)设OM=x.
当点C在点D右侧时,连接CM,过点A作AF⊥y轴于点F,
由∠BAM=∠DAF=90°,
可知:∠BAD=∠MAF;
∴在△BAD和△MAF中,
,
∴△BAD≌△MAF.
∴BD=FM=6-x.
又∵AC=AC,∠BAC=∠MAC,
∴△BAC≌△MAC.
∴BC=CM=8-x.
在Rt△COM中,由勾股定理得:
OC2+OM2=CM2,即42+x2=(8-x)2,
解得:x=3,
∴M点坐标为(0,3).
当点C在点D左侧时,连接CM,过点A作AF⊥y轴于点F,
同理,△BAD≌△MAF,
∴BD=FM=6+x.
同理,
△BAC≌△MAC,
∴BC=CM=4+x.
在Rt△COM中,由勾股定理得:
OC2+OM2=CM2,即82+x2=(4+x)2,
解得:x=6,
∴M点坐标为(0,-6).
 解:(1)∵AB=AC,∠BAC=45°,
解:(1)∵AB=AC,∠BAC=45°,∴∠ABC=∠ACB=67.5°.
过点A作AE⊥OB于E,
则△AEO是等腰直角三角形,∠EAO=45°.
∵AB=AC,AE⊥OB,
∴∠BAE=
| 1 |
| 2 |
∴∠BAO=67.5°=∠ABC,
∴OA=OB.
(2)设OM=x.
当点C在点D右侧时,连接CM,过点A作AF⊥y轴于点F,
由∠BAM=∠DAF=90°,
可知:∠BAD=∠MAF;
∴在△BAD和△MAF中,
|
∴△BAD≌△MAF.
∴BD=FM=6-x.
又∵AC=AC,∠BAC=∠MAC,
∴△BAC≌△MAC.
∴BC=CM=8-x.
在Rt△COM中,由勾股定理得:
OC2+OM2=CM2,即42+x2=(8-x)2,
解得:x=3,
∴M点坐标为(0,3).
当点C在点D左侧时,连接CM,过点A作AF⊥y轴于点F,
同理,△BAD≌△MAF,
∴BD=FM=6+x.
同理,
△BAC≌△MAC,
∴BC=CM=4+x.
在Rt△COM中,由勾股定理得:
OC2+OM2=CM2,即82+x2=(4+x)2,
解得:x=6,
∴M点坐标为(0,-6).
点评:本题考查了等腰三角形的性质以及全等三角形的判定与性质,和勾股定理的应用,正确进行分情况讨论,证明△BAD≌△MAF是关键.

练习册系列答案
相关题目
方程x2+6x=5的左边配成完全平方后所得方程为( )
| A、(x+3)2=14 |
| B、(x-3)2=14 |
| C、(x+6)2=12 |
| D、以上答案均不对 |
下列图形中,不属于对称图形的是( )
| A、圆 | B、扇形 |
| C、抛物线 | D、直角边长不相等的直角三角形 |
在△ABC中,AB=AC,BC=6,已知⊙O是△ABC的外接圆,且⊙O的半径为5,则AB是长为( )
A、
| ||||
B、3
| ||||
C、
| ||||
D、
|
若a-2b-3=0,则(a-2b)2-a+2b-5的值是( )
| A、-5 | B、-11 | C、7 | D、1 |
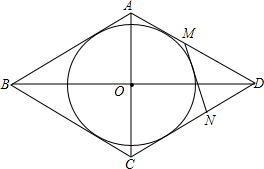 如图,已知菱形ABCD外切于圆O,MN是与AD、CD分别交于M、N的任意一条切线.求证:AM•CN为定值.
如图,已知菱形ABCD外切于圆O,MN是与AD、CD分别交于M、N的任意一条切线.求证:AM•CN为定值. 如图所示,正方形ABCD中,M是AD的中点,点N在DC上,且DN=
如图所示,正方形ABCD中,M是AD的中点,点N在DC上,且DN=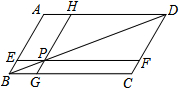 如图,在?ABCD中,过对角线BD上一点P作EF∥BC,GH∥AB,图中哪两个平行四边形面积相等?为什么?
如图,在?ABCD中,过对角线BD上一点P作EF∥BC,GH∥AB,图中哪两个平行四边形面积相等?为什么?