题目内容
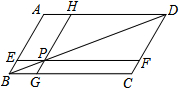 如图,在?ABCD中,过对角线BD上一点P作EF∥BC,GH∥AB,图中哪两个平行四边形面积相等?为什么?
如图,在?ABCD中,过对角线BD上一点P作EF∥BC,GH∥AB,图中哪两个平行四边形面积相等?为什么?考点:平行四边形的性质
专题:
分析:由条件可证明四边形HPFD、BEPG为平行四边形,可证明△PEB≌△BGP,△PHD≌△DFP,△ABD≌△CDB,再利用面积的和差可得出四边形AEPH和四边形PFCG的面积相等.
解答:解:四边形AEPH和四边形PFCG的面积相等,理由如下:
∵EF∥BC,GH∥AB,
∴四边形HPFD、BEPG为平行四边形,
∴PE=BG,BE=BG,
在△PEB和△BGP中,
,
∴△PEB≌△BGP(SSS),
∴S△PEB=S△BGP,
同理可得S△PHD=S△DFP,S△ABD=S△CDB,
∴S△ABD-S△PEB-S△PHD=S△CDB-S△BGP-S△DFP,
即S四边形AEPH=S四边形PFCG.
∵EF∥BC,GH∥AB,
∴四边形HPFD、BEPG为平行四边形,
∴PE=BG,BE=BG,
在△PEB和△BGP中,
|
∴△PEB≌△BGP(SSS),
∴S△PEB=S△BGP,
同理可得S△PHD=S△DFP,S△ABD=S△CDB,
∴S△ABD-S△PEB-S△PHD=S△CDB-S△BGP-S△DFP,
即S四边形AEPH=S四边形PFCG.
点评:本题主要考查平行四边形的判定和性质,掌握平行四边形的判定和性质是解题的关键,即①两组对边分别平行?四边形为平行四边形,②两组对边分别相等?四边形为平行四边形,③一组对边平行且相等?四边形为平行四边形,④两组对角分别相等?四边形为平行四边形,⑤对角线互相平分?四边形为平行四边形.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
 如图,在五边形ABCDE中,∠A+∠B+∠E=400°,∠BCD、∠CDE的平分线在五边形内相交于点O,∠1与∠2有怎样的数量关系?为什么?
如图,在五边形ABCDE中,∠A+∠B+∠E=400°,∠BCD、∠CDE的平分线在五边形内相交于点O,∠1与∠2有怎样的数量关系?为什么? 如图所示,推理填空.
如图所示,推理填空. 如图,已知?ABCD,过A作AM⊥BC于M,交BD于E,过C作CN⊥AD于N,交BD于F,连结AF、CE.求证:四边形AECF为平行四边形.
如图,已知?ABCD,过A作AM⊥BC于M,交BD于E,过C作CN⊥AD于N,交BD于F,连结AF、CE.求证:四边形AECF为平行四边形.