题目内容
已知直线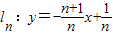 (n是正整数).当n=1时,直线l1:y=-2x+1与 x轴和y轴分别交于点A1和B1,设△A1OB1(O是平面直角坐标系的原点)的面积为s1;当n=2时,直线
(n是正整数).当n=1时,直线l1:y=-2x+1与 x轴和y轴分别交于点A1和B1,设△A1OB1(O是平面直角坐标系的原点)的面积为s1;当n=2时,直线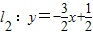 与x轴和y轴分别交于点A2和B2,设△A2OB2的面积为s2,…,依此类推,直线ln与x轴和y轴分别交于点An和Bn,设△AnOBn的面积为Sn.
与x轴和y轴分别交于点A2和B2,设△A2OB2的面积为s2,…,依此类推,直线ln与x轴和y轴分别交于点An和Bn,设△AnOBn的面积为Sn.(1)求△A1OB1的面积s1;
(2)求s1+s2+s3+…+s2011的值.
【答案】分析:(1)令n=1,求出直线l1与y轴的交点,再根据三角形的面积公式进行解答;
(2)分别令n=1,n=2求出直线l1、l2与y轴的交点及直线与y轴所围成的三角形的面积,找出规律即可得出Sn的值.
解答:解:(1)当n=1时,直线l1:y=-2x+1与 x轴和y轴的交点是A1( ,0)和B1(0,1)
,0)和B1(0,1)
所以OA1= ,OB1=1,
,OB1=1,
∴s1= ;
;
(2)当n=2时,直线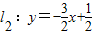 与 x轴和y轴的交点是A2(
与 x轴和y轴的交点是A2( ,0)和B2(0,
,0)和B2(0, )
)
所以OA2= ,OB2=
,OB2= ,
,
∴s2=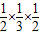 =
=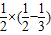
当n=3时,直线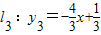 与 x轴和y轴的交点是A3(
与 x轴和y轴的交点是A3( ,0)和B3(0,
,0)和B3(0, )
)
所以OA3= ,OB3=
,OB3= ,
,
∴s3=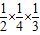 =
=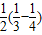
依此类推,sn=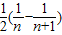
∴s1+s2+s3+…+s2011=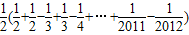
∴s1+s2+s3+…+s2011=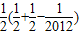
=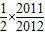
=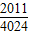 .
.
点评:本题考查的是一次函数的性质及三角形的面积公式,根据题意分别求出S1、S2、S3的值是解答此题的关键.
(2)分别令n=1,n=2求出直线l1、l2与y轴的交点及直线与y轴所围成的三角形的面积,找出规律即可得出Sn的值.
解答:解:(1)当n=1时,直线l1:y=-2x+1与 x轴和y轴的交点是A1(
 ,0)和B1(0,1)
,0)和B1(0,1)所以OA1=
 ,OB1=1,
,OB1=1,∴s1=
 ;
;(2)当n=2时,直线
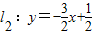 与 x轴和y轴的交点是A2(
与 x轴和y轴的交点是A2( ,0)和B2(0,
,0)和B2(0, )
)所以OA2=
 ,OB2=
,OB2= ,
,∴s2=
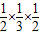 =
=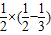
当n=3时,直线
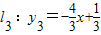 与 x轴和y轴的交点是A3(
与 x轴和y轴的交点是A3( ,0)和B3(0,
,0)和B3(0, )
)所以OA3=
 ,OB3=
,OB3= ,
,∴s3=
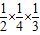 =
=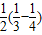
依此类推,sn=
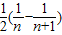
∴s1+s2+s3+…+s2011=
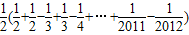
∴s1+s2+s3+…+s2011=
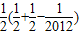
=
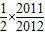
=
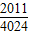 .
.点评:本题考查的是一次函数的性质及三角形的面积公式,根据题意分别求出S1、S2、S3的值是解答此题的关键.

练习册系列答案
相关题目
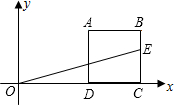 如图,正方形ABCD被直线OE分成面积相等的两部分,已知线段OD、AD的长都是正整数,
如图,正方形ABCD被直线OE分成面积相等的两部分,已知线段OD、AD的长都是正整数,| CE |
| BE |
| A、324 | B、331 |
| C、354 | D、361 |
 (n是正整数).当n=1时,直线l1:y=-2x+1与 x轴和y轴分别交于点A1和B1,设△A1OB1(O是平面直角坐标系的原点)的面积为s1;当n=2时,直线
(n是正整数).当n=1时,直线l1:y=-2x+1与 x轴和y轴分别交于点A1和B1,设△A1OB1(O是平面直角坐标系的原点)的面积为s1;当n=2时,直线 与x轴和y轴分别交于点A2和B2,设△A2OB2的面积为s2,…,依此类推,直线ln与x轴和y轴分别交于点An和Bn,设△AnOBn的面积为Sn.
与x轴和y轴分别交于点A2和B2,设△A2OB2的面积为s2,…,依此类推,直线ln与x轴和y轴分别交于点An和Bn,设△AnOBn的面积为Sn.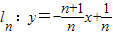 (n是正整数).当n=1时,直线l1:y=-2x+1与 x轴和y轴分别交于点A1和B1,设△A1OB1(O是平面直角坐标系的原点)的面积为s1;当n=2时,直线
(n是正整数).当n=1时,直线l1:y=-2x+1与 x轴和y轴分别交于点A1和B1,设△A1OB1(O是平面直角坐标系的原点)的面积为s1;当n=2时,直线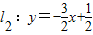 与x轴和y轴分别交于点A2和B2,设△A2OB2的面积为s2,…,依此类推,直线ln与x轴和y轴分别交于点An和Bn,设△AnOBn的面积为Sn.
与x轴和y轴分别交于点A2和B2,设△A2OB2的面积为s2,…,依此类推,直线ln与x轴和y轴分别交于点An和Bn,设△AnOBn的面积为Sn.