题目内容
8. 如图,在△ABC中,按以下步骤作图:
如图,在△ABC中,按以下步骤作图:①分别以点A、C为圆心,以大于$\frac{1}{2}$AC的长为半径画弧,两弧相交于M、N两点;
②作直线MN交BC于点D,连接AD,
若∠C=28°,AB=BD,则∠B的度数为68°.
分析 利用线段垂直平分线的性质得出AD=DC,再利用等腰三角形的性质结合三角形内角和定理得出答案.
解答 解:由题意可得:MN是AC的垂直平分线,
则AD=DC,故∠C=∠DAC,
∵∠C=28°,
∴∠DAC=28°,
∴∠ADB=56°,
∵AB=BD,
∴∠BAD=∠BDA=56°,
∴∠B=180°-56°-56°=68°.
故答案为:68°.
点评 此题主要考查了基本作图以及线段垂直平分线的性质,正确掌握线段垂直平分线的性质是解题关键.

练习册系列答案
相关题目
19.近似数8.01×104精确到( )
| A. | 万位 | B. | 百分位 | C. | 万分位 | D. | 百位 |
3.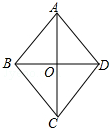 如图,菱形ABCD,AC与BD相交于点O,AC=8,BD=6,则菱形的边长AB是( )
如图,菱形ABCD,AC与BD相交于点O,AC=8,BD=6,则菱形的边长AB是( )
 如图,菱形ABCD,AC与BD相交于点O,AC=8,BD=6,则菱形的边长AB是( )
如图,菱形ABCD,AC与BD相交于点O,AC=8,BD=6,则菱形的边长AB是( )| A. | 10 | B. | 8 | C. | 6 | D. | 5 |
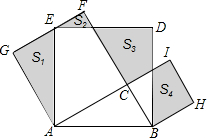 如图,Rt△ABC中,∠C=90°,AC=4,BC=3.分别以AB、AC、BC为边在AB的同侧作正方形ABDE、ACFG、BCIH,四块阴影部分的面积分别为S1、S2、S3、S4. 则S1+S2+S3+S4等于18.
如图,Rt△ABC中,∠C=90°,AC=4,BC=3.分别以AB、AC、BC为边在AB的同侧作正方形ABDE、ACFG、BCIH,四块阴影部分的面积分别为S1、S2、S3、S4. 则S1+S2+S3+S4等于18.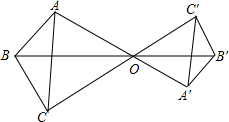 如图,BC∥B′C′,AC∥A′C′,求证:AB∥A′B′.
如图,BC∥B′C′,AC∥A′C′,求证:AB∥A′B′.