题目内容
(本题满分7分)如图,直角三角形的两直角边AC=6 cm,BC=8 cm,沿AD折叠使AC落在AB上.点C与E重合,折痕为AD,试求CD的长.

CD的长为3cm
【解析】
试题分析:由折叠的性质知CD=DE,AC=AE.根据题意在Rt△BDE中运用勾股定理求DE.
试题解析:∵△ABC是直角三角形,AC=6cm,BC=8cm,
∴AB= (cm),
(cm),
∵△AED是△ACD翻折而成,
∴AE=AC=6cm,
设DE=CD=xcm,∠AED=90°,
∴BE=AB-AE=10-6=4cm,
在Rt△BDE中,BD2=DE2+BE2,
即(8-x)2=42+x2,
解得x=3.
故CD的长为3cm.
考点:折叠的性质,勾股定理

练习册系列答案
 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
(本题6分)某校从甲乙两名优秀选手中选一名选手参加全市中学生田径百米比赛(100米记录为12.2秒,通常情况下成绩为12.5秒可获冠军)。该校预先对这两名选手测试了8次,测试成绩如下表:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
选手甲成绩(秒) | 12.1 | 12.4 | 12.8 | 12.5 | 13 | 12.6 | 12.4 | 12.2 |
选手乙成绩(秒) | 12 | 11.9 | 12.8 | 13 | 13.2 | 12.8 | 11.8 | 12.5 |
根据测试成绩,请你运用所学过的统计知识做出合理的判断,派哪一位选手参加比赛更好?为什么?

 .(在横线上填“<”或“>”)
.(在横线上填“<”或“>”)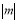 =3,
=3, =5且m-n>0,则m+n的值是 ( )
=5且m-n>0,则m+n的值是 ( )

 B.
B.  C.
C. D.
D. 