题目内容
11.解方程组:(1)$\left\{{\begin{array}{l}{x=y+1}\\{2x+y=2}\end{array}}\right.$
(2)$\left\{{\begin{array}{l}{5x-2y=4}\\{2x-3y=-5}\end{array}}\right.$.
分析 (1)方程组利用代入消元法求出解即可;
(2)方程组利用加减消元法求出解即可.
解答 解:(1)$\left\{\begin{array}{l}{x=y+1①}\\{2x+y=2②}\end{array}\right.$,
①代入②得:2y+2+y=2,
解得:y=0,
把y=0代入①得:x=1,
则方程组的解为$\left\{\begin{array}{l}{x=1}\\{y=0}\end{array}\right.$;
(2)$\left\{\begin{array}{l}{5x-2y=4①}\\{2x-3y=-5②}\end{array}\right.$,
①×3-②×2得:11x=22,即x=2,
把x=2代入①得:y=3,
则方程组的解为$\left\{\begin{array}{l}{x=2}\\{y=3}\end{array}\right.$.
点评 此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
20.若多项式ax2+bx+c因式分解的结果为(x-2)(x+4),则abc的值为( )
| A. | -16 | B. | 16 | C. | 8 | D. | -8 |
 如图,所有小正方形的边长都为1,A、B、C都在格点上.
如图,所有小正方形的边长都为1,A、B、C都在格点上. 如图,长方形ABCD中,长BC=a,宽AB=b,(b<a<2b),四边形ABEH和四边形ECGF都是正方形.
如图,长方形ABCD中,长BC=a,宽AB=b,(b<a<2b),四边形ABEH和四边形ECGF都是正方形. 如图,从A处到B处,选择第②条路最近.理由是两点之间,线段最短.
如图,从A处到B处,选择第②条路最近.理由是两点之间,线段最短.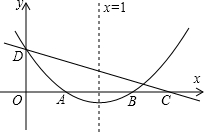 如图,直线y=kx+c与抛物线y=ax2+bx+c的图象都经过y轴上的D点,抛物线与x轴交于AB两点,其对称轴为直线x=1,且OA=OD,直线y=kx+c与x轴交于点C(点C在点B的右侧).则下列命题中正确的个数是( )
如图,直线y=kx+c与抛物线y=ax2+bx+c的图象都经过y轴上的D点,抛物线与x轴交于AB两点,其对称轴为直线x=1,且OA=OD,直线y=kx+c与x轴交于点C(点C在点B的右侧).则下列命题中正确的个数是( )