题目内容
2.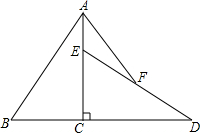 如图,已知Rt△ABC中,∠ACB=90°,AC=6,BC=4,将△ABC绕直角顶点C顺时针旋转90°得到△DEC,若点F是DE的中点,连接AF,则AF=( )
如图,已知Rt△ABC中,∠ACB=90°,AC=6,BC=4,将△ABC绕直角顶点C顺时针旋转90°得到△DEC,若点F是DE的中点,连接AF,则AF=( )| A. | $\sqrt{13}$ | B. | 5 | C. | $\sqrt{13}$+2 | D. | 3$\sqrt{2}$ |
分析 相办法把AF放入直角三角形当中,于是过点F作FH垂直AC于H,过点F作FG垂直CD于G,算出HF和AH即可求出AF.
解答 解:如图,过点F作FH垂直AC于H,过点F作FG垂直CD于G,
由旋转的性质可知:CD=CA=6,CE=CB=4,
∵F为ED中点,
∴GF=CH=EH=2,HF=CG=GD=3,
∴AH=AC-CH=6-2=4,
由勾股定理可知:AF=$\sqrt{16+9}=5$.
故选B.
点评 本题考查了旋转的性质、中位线定理、勾股定理等知识点,难度不大.清楚旋转的“不变”特征是解答的关键.

练习册系列答案
相关题目
7.下列计算正确的是( )
| A. | 2a•4a=8a | B. | a2+a1=a3 | C. | (a2)3=a5 | D. | a1•a1=a2 |
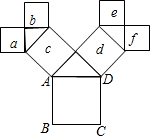 如图,所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形a,b,c,d,e,f的面积和为32,则最大的正方形ABCD的边长为4.
如图,所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形a,b,c,d,e,f的面积和为32,则最大的正方形ABCD的边长为4.
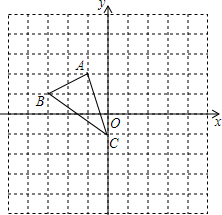 如图,在平面直角坐标系网格中,△ABC的顶点都在格点上,点C坐标(0,-1).
如图,在平面直角坐标系网格中,△ABC的顶点都在格点上,点C坐标(0,-1).