题目内容
 如图,一只船自西向东航行,上午10时到一座灯塔P的南偏西60°距塔68海里的M处,下午2时到达这座灯塔的南偏东60°的N处,求这只船航行的速度?(
如图,一只船自西向东航行,上午10时到一座灯塔P的南偏西60°距塔68海里的M处,下午2时到达这座灯塔的南偏东60°的N处,求这只船航行的速度?(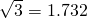 ,精确到0.1海里).
,精确到0.1海里).
解:在Rt△APM中,PM=68海里,∠APM=60°,
∴AM=PM•sin60°=34 (海里),
(海里),
∵在△PMA和△PNA中,
 ,
,
∴△PMA≌△PNA(ASA),
∴AN=AM=34 (海里),
(海里),
∴MN=AM+AN=68 (海里),
(海里),
∴68 ÷4≈29.4(海里/小时).
÷4≈29.4(海里/小时).
答:这只船航行的速度29.4海里/小时.
分析:由在Rt△APM中,PM=68海里,∠APM=60°,利用三角函数的知识即可求得AM的长,易证得△PMA≌△PNA,即可得AN=AM,继而求得MN的长,则可求得这只船航行的速度.
点评:此题考查了方向角问题以及全等三角形的判定与性质.此题难度适中,注意利用解直角三角形的知识求解是解此题的关键.
∴AM=PM•sin60°=34
 (海里),
(海里),∵在△PMA和△PNA中,
 ,
,∴△PMA≌△PNA(ASA),
∴AN=AM=34
 (海里),
(海里),∴MN=AM+AN=68
 (海里),
(海里),∴68
 ÷4≈29.4(海里/小时).
÷4≈29.4(海里/小时).答:这只船航行的速度29.4海里/小时.
分析:由在Rt△APM中,PM=68海里,∠APM=60°,利用三角函数的知识即可求得AM的长,易证得△PMA≌△PNA,即可得AN=AM,继而求得MN的长,则可求得这只船航行的速度.
点评:此题考查了方向角问题以及全等三角形的判定与性质.此题难度适中,注意利用解直角三角形的知识求解是解此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,一只船自西向东航行,上午9时到达一座灯塔P的西南方向68海里的M处,上午11时到达这座灯塔的正南方向N处,求这只船航行的速度.
如图,一只船自西向东航行,上午9时到达一座灯塔P的西南方向68海里的M处,上午11时到达这座灯塔的正南方向N处,求这只船航行的速度. 如图,一只船自西向东航行,上午10时到一座灯塔P的南偏西60°距塔68海里的M处,下午2时到达这座灯塔的南偏东60°的N处,求这只船航行的速度?(
如图,一只船自西向东航行,上午10时到一座灯塔P的南偏西60°距塔68海里的M处,下午2时到达这座灯塔的南偏东60°的N处,求这只船航行的速度?( 如图,一只船自西向东航行,上午9时到达一座灯塔P的西南方向68海里的M处,上午11时到达这座灯塔的正南方向N处,求这只船航行的速度.
如图,一只船自西向东航行,上午9时到达一座灯塔P的西南方向68海里的M处,上午11时到达这座灯塔的正南方向N处,求这只船航行的速度. 如图,一只船自西向东航行,上午9时到达一座灯塔P的西南方向68海里的M处,上午11时到达这座灯塔的正南方向N处,求这只船航行的速度.
如图,一只船自西向东航行,上午9时到达一座灯塔P的西南方向68海里的M处,上午11时到达这座灯塔的正南方向N处,求这只船航行的速度.