题目内容
3．
如图，AB是⊙O的直径，∠BAD=70°，则∠ACD的度数是（ ）| A． | 20° | B． | 15° | C． | 35° | D． | 70° |
分析 首先连接BD，由AB是⊙O的直径，可求得∠ADB=90°，又由∠BAD=70°，求得∠B的度数，继而求得答案．
解答 
解：连接BD，
∵AB是⊙O的直径，
∴∠ADB=90°，
∵∠BAD=70°，
∴∠B=90°-∠BAD=20°，
∴∠ACD=∠B=20°．
故选A．
点评 此题考查了圆周角定理．注意准确作出辅助线是解此题的关键．
练习册系列答案
相关题目
13．
如图，在△ABC中，AD⊥BC，垂足为点D，若AC=6$\sqrt{2}$，∠C=45°，tan∠ABC=3，则BD等于（ ）
如图，在△ABC中，AD⊥BC，垂足为点D，若AC=6$\sqrt{2}$，∠C=45°，tan∠ABC=3，则BD等于（ ）| A． | 2 | B． | 3 | C． | 3$\sqrt{2}$ | D． | 2$\sqrt{3}$ |
14．
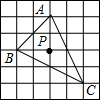△ABC在正方形网格中的位置如图所示，点A，B，C，P均在格点上，则点P是△ABC的（ ）
△ABC在正方形网格中的位置如图所示，点A，B，C，P均在格点上，则点P是△ABC的（ ）| A． | 三条垂直平分线的交点 | B． | 三条内角角平分线的交点 | ||
| C． | 重心 | D． | 无法确定 |
三国时期吴国赵爽创制了“勾股圆方图”（如图）证明了勾股定理．在这幅“勾股圆方图”中，大正方形ABCD是由4个全等的直角三角形再加上中间的那个小正方形EFGH组成的．若小正方形的边长是1，每个直角三角形的短的直角边长是3，则大正方形ABCD的面积是25．
18．方程1-3x=0的解是（ ）
| A． | x=-$\frac{1}{3}$ | B． | x=$\frac{1}{3}$ | C． | x=-3 | D． | x=3 |
8．下列说法正确的是（ ）
| A． | 任何有理数有倒数 | B． | -a一定是负数 | ||
| C． | 立方等于它本身的数有±1 | D． | 绝对值最小的数是0 |
如图，|a-b|-$\sqrt{{b}^{2}}$=a．
6．
如图，在△ABC中，DE∥BC交AB于点D，交AC于点E．若AB=4，AC=3，AD=3，则AE的长为（ ）
如图，在△ABC中，DE∥BC交AB于点D，交AC于点E．若AB=4，AC=3，AD=3，则AE的长为（ ）| A． | $\frac{4}{9}$ | B． | $\frac{3}{4}$ | C． | $\frac{4}{3}$ | D． | $\frac{9}{4}$ |