��Ŀ����
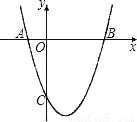
��ͼ��������y=x2+bx+c��x�ύ��A����1��0����B��3��0�����㣮
��1����b��c��ֵ��
��2��PΪ�������ϵĵ㣬������S��PAB=8����P������꣮
��ϰ��ϵ�д�
 ��˼ά������ҵ��ټ��ִ�ѧ������ϵ�д�
��˼ά������ҵ��ټ��ִ�ѧ������ϵ�д� �����������Ż�ѧϰϵ�д�
�����������Ż�ѧϰϵ�д�
�����Ŀ
��Ŀ����
��ͼ��������y=x2+bx+c��x�ύ��A����1��0����B��3��0�����㣮
��1����b��c��ֵ��
��2��PΪ�������ϵĵ㣬������S��PAB=8����P������꣮

 ��˼ά������ҵ��ټ��ִ�ѧ������ϵ�д�
��˼ά������ҵ��ټ��ִ�ѧ������ϵ�д� �����������Ż�ѧϰϵ�д�
�����������Ż�ѧϰϵ�д�