题目内容
5.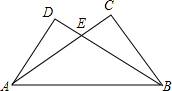 如图,在△ABC和△BAD中,AC与BD相交于点E,已知AD=BC,另外只能从下面给出的三个条件①∠DAB=∠CBA,②∠D=∠C ③∠DBA=∠CAB 选择其中的一个用来证明在△ABC和△BAD全等,这个条件是①.(填写编号),并证明△ABC≌△BAD.
如图,在△ABC和△BAD中,AC与BD相交于点E,已知AD=BC,另外只能从下面给出的三个条件①∠DAB=∠CBA,②∠D=∠C ③∠DBA=∠CAB 选择其中的一个用来证明在△ABC和△BAD全等,这个条件是①.(填写编号),并证明△ABC≌△BAD.
分析 选择条件①,根据全等三角形的判定定理SAS进行证明即可.
解答 解:这个条件是:①,证明如下:
在△ABD与△BAC中,
$\left\{\begin{array}{l}{BC=AD}\\{∠CBA=∠DAB}\\{BA=AB}\end{array}\right.$,
∴△ABC≌△BAD(SAS).
点评 本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
相关题目
16.在证明过程中,可以用来作为推理依据的是( )
| A. | 公理 定义 | B. | 定理 定义 公理 | C. | 公理 | D. | 定理 公理 |
20.已知点A(a,-3),B(4,b)关于y轴的对称,则a+b的值为( )
| A. | 1 | B. | 7 | C. | -7 | D. | -1 |
17.已知⊙O1的半径为3cm,⊙O2的半径为5cm,圆心距O1O2为2cm,则⊙O1和⊙O2的位置关系是( )
| A. | 相交 | B. | 外离 | C. | 外切 | D. | 内切 |
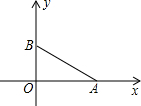 如图,在直角坐标系中有两点A(4,0),B(0,2)如果C在x轴上(C点与A不重合),当C点坐标为(-1,0) 或(1,0)时,使得由点B,O,C构成的三角形与△AOB相似(至少找出两个满足条件点).
如图,在直角坐标系中有两点A(4,0),B(0,2)如果C在x轴上(C点与A不重合),当C点坐标为(-1,0) 或(1,0)时,使得由点B,O,C构成的三角形与△AOB相似(至少找出两个满足条件点).