Question

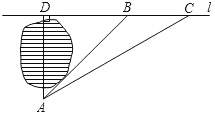
【题目】如图，用长33米的竹篱笆围成一个矩形院墙，其中一面靠墙，墙长15米，墙的对面有一个2米宽的门，设垂直于墙的一边长为米，院墙的面积为平方米．

（1）直接写出与的函数关系式；

（2）若院墙的面积为143平方米，求的值；

（3）若在墙的对面再开一个宽为米的门，且面积的最大值为165平方米，求的值．

Answer 1

【答案】（1）；（2）的值为11；（3）的值为2米

【解析】

（1）根据矩形面积公式可写出函数关系式；

（2）根据（1）所得的关系，将S=143代入即可求解；

（3）再开一个宽为a的门，即矩形的另一边长为m，根据矩形的面积公式即可求解.

解：（1）根据题意得：；

（2）当时，即，

解得：，，

墙长15米，

，

的值为11；

（3），

面积取得最大值为，

，

把代入，得

解得．

答：的值为2米．