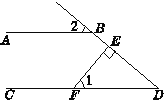
题目内容
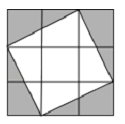
如图,在

 ,
,






























练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知二次函数y=ax2+bx(a≠0)中自变量x和函数值y的部分对应值如下表:
x | … | ﹣2.5 | ﹣2 | ﹣1 | 0 | 0.5 | … |
y | … | ﹣5 | 0 | 4 | 0 | ﹣5 | … |
(1)求二次函数解析式,并写出顶点坐标;
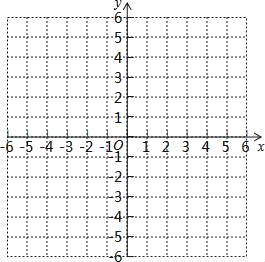
(2)在直角坐标系中画出该抛物线的图象;
(3)若该抛物线上两点A(x1,y1)、B(x2,y2)的横坐标满足x1<x2<﹣1,试比较y1与y2的大小,并说明理由.



 – 2 )0-
– 2 )0-
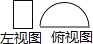 B.
B.  C.
C.  D.
D. 
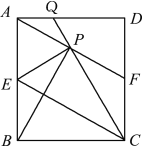
 B.
B. 
 D.
D. 
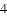
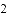
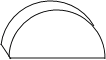
 ,PC=1,求图中阴影部分的面积.(结果保留π)
,PC=1,求图中阴影部分的面积.(结果保留π)