题目内容
如图，把一张长方形纸条ABCD沿AF折叠，已知∠ADB=15°，若AE∥BD，则∠EFC=________度．
105
分析：由题意AE∥BD，根据内错角相等，可知∠AEF=∠HGD=90°，从而求出∠EFC的度数．
解答：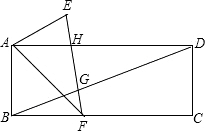
解：设EF与BD相交于G点，与AD相交于H点，
∵AE∥BD，
∴∠AEF=∠HGD=90°，
则∠FHD=75°，
故结果为∠EFC=105°．
故答案为：105°．
点评：此题考查折叠图形的性质及利用平行线的性质来解题，比较简单．
分析：由题意AE∥BD，根据内错角相等，可知∠AEF=∠HGD=90°，从而求出∠EFC的度数．
解答：
解：设EF与BD相交于G点，与AD相交于H点，∵AE∥BD，
∴∠AEF=∠HGD=90°，
则∠FHD=75°，
故结果为∠EFC=105°．
故答案为：105°．
点评：此题考查折叠图形的性质及利用平行线的性质来解题，比较简单．
练习册系列答案
相关题目
如图，把一张长方形的纸按图那样折叠后，B、D两点落在B′、D′点处，若得∠AOB′=70°，则∠B′OG的度数为
如图，把一张长方形的纸按图那样折叠后，B、D两点落在B′、D′点处，若∠AOB′=85°，则∠CGO的度数为
如图，把一张长方形的纸按图那样折叠后，B、D两点落在B′、D′点处，若∠AOB′=70°，则∠B′OG的度数为
如图，将一张长方形纸斜折过去，使顶点A落在A’处，BC为折痕，然后再把BE折过去，使之与BA’重合，折痕为BD，求两折痕BC、BD的夹角∠CBD是多少度？