题目内容
如图，把一张长方形的纸按图那样折叠后，B、D两点落在B′、D′点处，若∠AOB′=85°，则∠CGO的度数为47.5
47.5
°．分析：根据∠AOB′=85°，可求出∠B'OB的度数，根据折叠的性质可得∠B'0G=∠BOG，然后根据平行线的性质可得∠BOG=∠CGO，即可求解．
解答：解：∵∠AOB′=85°，
∴∠B'OB=180°-∠AOB′=95°，
根据折叠的性质可得：∠B'0G=∠BOG，
∵∠B'OB=∠B'0G+∠BOG，
∴∠BOG=
×95°=47.5°，
∵AB∥CD，
∴∠CGO=∠OBG=47.5°．
故答案为：47.5．
∴∠B'OB=180°-∠AOB′=95°，
根据折叠的性质可得：∠B'0G=∠BOG，
∵∠B'OB=∠B'0G+∠BOG，
∴∠BOG=
| 1 |
| 2 |
∵AB∥CD，
∴∠CGO=∠OBG=47.5°．
故答案为：47.5．
点评：本题考查了平行线的性质以及折叠的性质，解答本题的关键是掌握平行线的性质：两直线平行，内错角相等．
练习册系列答案
相关题目
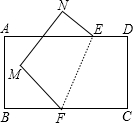如图，把一张长方形的纸片沿着EF折叠，点C、D分别落在M、N的位置，且∠MFB=| 1 |
| 2 |
| A、30° | B、36° |
| C、45° | D、72° |
如图，把一张长方形的纸片ABCD沿BD对折，使C点落在E点处，BE与AD相交于点O，图中除了△ABD≌△CDB外，请写出其他一组全等三角形