题目内容
数学活动课上,老师向同学们讲学校正在规划筹建周长为400m的跑道的消息,鼓励同学们试着给要建的跑道画一个示意图.要求跑道的两端是半圆形,中间是直线跑道,且跑道中间矩形面积最大.下面是四位同学给出的示意图,你认为正确的是
- A.

- B.

- C.

- D.

B
分析:先设矩形的长为xm,半圆的直径是d,中间的矩形区域面积是Sm2,则S=dx,且2x+πd=400;而S=dx= •πd•2x≤
•πd•2x≤
 ,可得最大值以及对应的d、x的值,即可求出答案.
,可得最大值以及对应的d、x的值,即可求出答案.
解答:设矩形的长为xm,半圆的直径是d,中间的矩形区域面积是Sm2,根据题意,知
S=dx,且2x+πd=400.
S=dx= •πd•2x≤
•πd•2x≤
 =
= ,
,
当且仅当πd=2x=200,即x=100时等号成立,此时,d= ,
,
所以,应设计矩形的长为100m,宽约为63.7m时,矩形面积最大;
故选B.
点评:本题考查了二次函数的应用;解题的关键是根据基本不等式a+b≥2 ,(其中a>0,b>0)进行变形应用,或者用二次函数的性质解答也可以.
,(其中a>0,b>0)进行变形应用,或者用二次函数的性质解答也可以.
分析:先设矩形的长为xm,半圆的直径是d,中间的矩形区域面积是Sm2,则S=dx,且2x+πd=400;而S=dx=
 •πd•2x≤
•πd•2x≤
 ,可得最大值以及对应的d、x的值,即可求出答案.
,可得最大值以及对应的d、x的值,即可求出答案.解答:设矩形的长为xm,半圆的直径是d,中间的矩形区域面积是Sm2,根据题意,知
S=dx,且2x+πd=400.
S=dx=
 •πd•2x≤
•πd•2x≤
 =
= ,
,当且仅当πd=2x=200,即x=100时等号成立,此时,d=
 ,
,所以,应设计矩形的长为100m,宽约为63.7m时,矩形面积最大;
故选B.
点评:本题考查了二次函数的应用;解题的关键是根据基本不等式a+b≥2
 ,(其中a>0,b>0)进行变形应用,或者用二次函数的性质解答也可以.
,(其中a>0,b>0)进行变形应用,或者用二次函数的性质解答也可以. 
练习册系列答案
相关题目
 向上,请你根据以上数据,帮助小明同学计算出这条河的宽度.(参考数据:sin20°≈
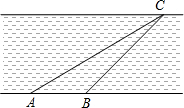
向上,请你根据以上数据,帮助小明同学计算出这条河的宽度.(参考数据:sin20°≈ 在一次数学活动课上,老师带领学生去测长江的宽度,某学生在长江北岸点A处观测到长江对岸水边有一点C,测得C在A东南方向上,沿长江边向东前行200米到达B处,测得C在B南偏东30°的方向上.
在一次数学活动课上,老师带领学生去测长江的宽度,某学生在长江北岸点A处观测到长江对岸水边有一点C,测得C在A东南方向上,沿长江边向东前行200米到达B处,测得C在B南偏东30°的方向上.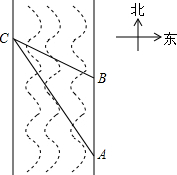 (2012•富宁县模拟)在一次数学活动课上,老师带领学生去测一条南北流向河流的河宽,如图所示,某学生在河东岸点A处观测河对岸水边点C,测得C在A北偏西30°的方向上,沿河岸向北前行20米到达B处,测得C在B北偏西60°的方向上.请你根据以上数据,帮助该同学计算出这条河的宽度.(精确到0.1,参考数据:
(2012•富宁县模拟)在一次数学活动课上,老师带领学生去测一条南北流向河流的河宽,如图所示,某学生在河东岸点A处观测河对岸水边点C,测得C在A北偏西30°的方向上,沿河岸向北前行20米到达B处,测得C在B北偏西60°的方向上.请你根据以上数据,帮助该同学计算出这条河的宽度.(精确到0.1,参考数据: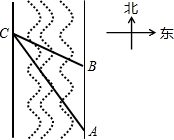 在一次数学活动课上,老师带领学生去测一条南北流向河流的河宽,如图所示,某学生在河东岸点A处观测河对岸水边点C,测得C在A北偏西30°的方向上,沿河岸向北前行30米到达B处,测得C在B北偏西60°的方向上,请你根据以上数据,帮助该同学计算出这条河的宽度.(答案带根号)
在一次数学活动课上,老师带领学生去测一条南北流向河流的河宽,如图所示,某学生在河东岸点A处观测河对岸水边点C,测得C在A北偏西30°的方向上,沿河岸向北前行30米到达B处,测得C在B北偏西60°的方向上,请你根据以上数据,帮助该同学计算出这条河的宽度.(答案带根号)